Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a) Ta thấy: $\frac{3}{9}=\frac{4}{12}=\frac{5}{15}$
$\Leftrightarrow \frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CA}{C'A'}$
$\Rightarrow \triangle ABC\sim \triangle A'B'C'$ (c.c.c)
b)
\(\frac{8}{8}=\frac{9}{9}\Leftrightarrow \frac{BC}{A'B'}=\frac{CA}{B'C'}=1\). Tỷ số này khác với $\frac{AB}{C'A'}(=\frac{7}{12})$
Nên không tồn tại 2 tam giác đồng dạng trong TH này.

a) Hai tam giác đồng dạng với nhau vì \(\dfrac{40}{8}=\dfrac{50}{10}=\dfrac{60}{12}\) (cùng bằng 5)
b) Hai tam giác không đồng dạng với nhau vì \(\dfrac{3}{9}\ne\dfrac{4}{15}\)
c) Hai tam giác đồng dạng với nhau vì \(\dfrac{1}{2}=\dfrac{1}{2}=\dfrac{0,5}{1}\)

Lời giải:
a) Ta thấy:
$\frac{4}{8}=\frac{5}{10}=\frac{6}{12}$ nên 2 tam giác đồng dạng theo TH c.c.c
b) Pitago: $A'C'=\sqrt{B'C'^2-A'B'^2}=\sqrt{16^2-9^2}=5\sqrt{7}$
Xét tam giác $ABC$ và $A'B'C'$ có:
$\widehat{A}=\widehat{A'}=90^0$
$\frac{AB}{AC}\neq \frac{A'B'}{A'C'}$
Do đó 2 tam giác không đồng dạng

Áp dụng định lý Pytago, ta có
32+42= 25
Cạnh huyền= \(\sqrt{ }\)25 = 5

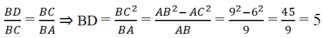
a. Đúng
b. Sai
c. Sai
d. Đúng