Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x, y (giờ) lần lượt là thời gian mà người thứ nhất và người thứ hai một mình xây xong bức tường.
Điều kiện: 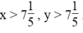
Như vậy, trong 1 giờ người thứ nhất xây được 1/x (bức tường), người thứ hai xây được 1/y (bức tường).
Trong 1 giờ, cả hai người xây được 1: 36/5 = 5/36 (bức tường)
Ta có phương trình: 1/x + 1/y = 5/36
Nếu người thứ nhất làm trong 5 giờ và người thứ hai làm trong 6 giờ thì cả hai xây được 3/4 bức tường, ta có phương trình: 5/x + 6/y = 3/4
Ta có hệ phương trình: 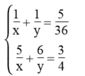
Đặt m = 1/x , n = 1/y , ta có:
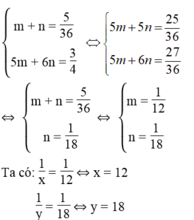
Giá trị của x và y thỏa điều kiện bài toán.
Vậy người thứ nhất làm một mình xong bức tường trong 12 giờ, người thứ hai làm một mình xong bức tường trong 18 giờ.

Mình có nghĩ ra đáp án ko biêt đung ko, mình mơi tham gia diễn đàn, có một số kí hiệu chưa biết gõ . Gọi x là thơi gian lam xong cua ngươi 1, Khi đó thơi gian lam xong cua ngươi 2 là x+5. Trong 1 ngay nguoi 1 lam dươc 1

Gọi x(giờ) là thời gian người thứ nhất hoàn thành công việc khi làm riêng
Gọi y(giờ) là thời gian người thứ hai hoàn thành công việc khi làm riêng
(Điều kiện: x>6; y>6)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người làm được: \(\dfrac{1}{6}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)(1)
Vì khi người thứ nhất làm trong 3 giờ và người thứ hai làm trong 7 giờ thì hai người hoàn thành \(\dfrac{2}{3}\) công việc nên ta có phương trình:
\(\dfrac{3}{x}+\dfrac{7}{y}=\dfrac{2}{3}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{3}{x}+\dfrac{7}{y}=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{1}{2}\\\dfrac{3}{x}+\dfrac{7}{y}=\dfrac{2}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{4}{y}=-\dfrac{1}{6}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-6\cdot\left(-4\right)}{1}=24\\\dfrac{1}{x}+\dfrac{1}{24}=\dfrac{1}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{6}-\dfrac{1}{24}=\dfrac{1}{8}\\y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=24\end{matrix}\right.\)(thỏa ĐK)
Vậy: Người thứ nhất cần 8 giờ để hoàn thành công việc khi làm một mình
Người thứ hai cần 24 giờ để hoàn thành công việc khi làm một mình
Gọi thời gian người thứ nhất xây một mình xong bức tường là \(x\) (giờ), thời gian người thứ hai xây một mình xong bức tường là \(y\) (giờ); \(x>0;y>0\). Coi toàn bộ công việc như một đơn vị công việc.