Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

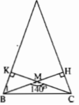
+) Xét tam giác vuông BKM có ∠BMC là góc ngoài tam giác tại đỉnh M nên:


1. Hai góc đối đỉnh thì bằng nhau, đúng
2. Hai góc bằng nhau thì đối đỉnh, sai
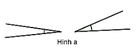
Vì tồn tại hai góc bằng nhau mà không chung đỉnh thì đó không phải hai góc đối đỉnh như hình sau:
3. Nếu M là trung điểm của AB thì MA = MB, đúng
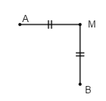
4. Nếu có MA = MB thì M là trung điểm của AB, sai
Vì nếu M, A, B không thẳng hàng thì MA = MB không suy ra được M là trung điểm của A
B.
5. Hai đường thẳng vuông góc thì cắt nhau, đúng
6. Hai đường thẳng cắt nhau thì vuông góc, sai
Vì hai đường thẳng cắt nhau không tạo thành góc vuông thì chúng không phải là hai đường thẳng vuông góc.
Chọn đáp án C

a: \(\widehat{MAQ}=180^0-60^0=120^0\)
\(\widehat{NAQ}=60^0\)

a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC(Cạnh huyền-góc nhọn)
Suy ra: AD=AE(Hai cạnh tương ứng)
hay A nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AE+EB=AB(E nằm giữa A và B)
AD+DC=AC(D nằm giữa A và C)
mà AE=AD(cmt)
và AB=AC(ΔABC cân tại A)
nên EB=DC
Xét ΔEBH vuông tại E và ΔDCH vuông tại D có
EB=DC(cmt)
\(\widehat{EBH}=\widehat{DCH}\)(ΔABD=ΔACE)
Do đó: ΔEBH=ΔDCH(Cạnh góc vuông-góc nhọn kề)
Suy ra: HE=HD(Hai cạnh tương ứng)
hay H nằm trên đường trung trực của ED(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AH là đường trung trực của ED
hay AH\(\perp\)ED(đpcm)

Ta sử dụng tính chất: hai tia phân giác của hai góc kề bù thì vuông góc với nhau
+) BM; BI là 2 tia p/g của góc B trong và ngoài tam giác => BM | BI => góc MBI = 90o
CN và CI là 2 tia p/g của góc C trong và ngoài tam giác ABC => CN | CI => góc ICN = 90o
+) Xét tam giác MBC có: góc M + MCB + MBC = 180o => góc M + MCB + (MBI + IBC) = 180o
=> góc M + góc \(\frac{C}{2}\) + góc \(\frac{B}{2}\) + 90o = 180o => góc M + góc \(\frac{B+C}{2}\) = 90o => góc M = 90o - góc \(\frac{B+C}{2}\) = \(\frac{180^o-\left(B+C\right)}{2}=\frac{A}{2}\)
+) tương tự, ta có góc N = góc A/2
Vậy góc M = Góc N = góc A/2
b) đã làm ở bài trên
góc M1+góc M2=180 độ
3 góc M1-7 góc M2=0
=>góc M1=126 độ, góc M2=54 độ