Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Ta có \(F=k\dfrac{\left|q_1q_2\right|}{r^2}=9.10^9.\dfrac{q_1^2}{r^2}\) \(\Leftrightarrow q_1=\sqrt{\dfrac{r^2.F}{9.10^9}}=\sqrt{\dfrac{0,02^2.10^{-6}}{9.10^9}}\)
\(\Leftrightarrow q_1=q_2=2,1.10^{-10}\left(C\right)\)
b. \(F'=k\dfrac{q_1^2}{r'^2}\Leftrightarrow r'=\sqrt{\dfrac{k.q_1^2}{F'}}=\sqrt{\dfrac{9.10^9.\left(2,1.10^{-10}\right)^2}{5.10^{-6}}}\) \(\Leftrightarrow r'=8,9.10^{-3}\left(m\right)=0,89\left(cm\right)\)

a) hai điện tích như nhau=> hai điện tích có độ lớn bằng nhau=> |q1|=|q2|=q
Và hai điện tích đẩy nhau nên hai điện tích cùng dấu.
\(F_1=\frac{k.\left|q_1.q_2\right|}{r^2}\Leftrightarrow10^{-5}=\frac{9.10^9.\left|q^2\right|}{\left(0,04\right)^2}\Rightarrow q=1,33.10^{-9}C\)
b) \(\frac{F_1}{F_2}=\frac{r_2^2}{r_1^2}\Leftrightarrow\frac{10^{-5}}{2,5.10^{-6}}=\frac{r_2^2}{0,o4^2}\Rightarrow r_2\approx0,08m=8cm\)

1.2/
\(F=\dfrac{k\left|q_1q_2\right|}{r^2}=\dfrac{kq^2}{r^2}\Leftrightarrow\dfrac{9.10^9.q^2}{0,04^2}=10^{-5}\Rightarrow q\approx1,33.10^{-9}\left(C\right)\)
\(r'^2=\dfrac{9.10^9.\left(1,33.10^{-9}\right)^2}{2,5.10^{-6}}=...\Rightarrow r=...\left(m\right)\)
2.2/ \(F=\dfrac{k\left|q_1q_2\right|}{r^2}\Leftrightarrow\left|q_1q_2\right|=\dfrac{1,8.1^2}{9.10^9}=...\)
Đẩy nhau=> 2 điện tích cùng dấu \(\Rightarrow q_1q_2=\dfrac{1,8}{9.10^9}\Leftrightarrow q_2=\dfrac{1,8}{9.10^9.q_1}\)
\(\Rightarrow\left\{{}\begin{matrix}q_1+q_2=3.10^{-5}\\q_2=\dfrac{1,8}{9.10^9.q_1}\end{matrix}\right.\Rightarrow...\)
P/s: Số xấu lắm, với cả tui hiện ko có cầm máy tính nên bạn tự tính nốt nhó :)
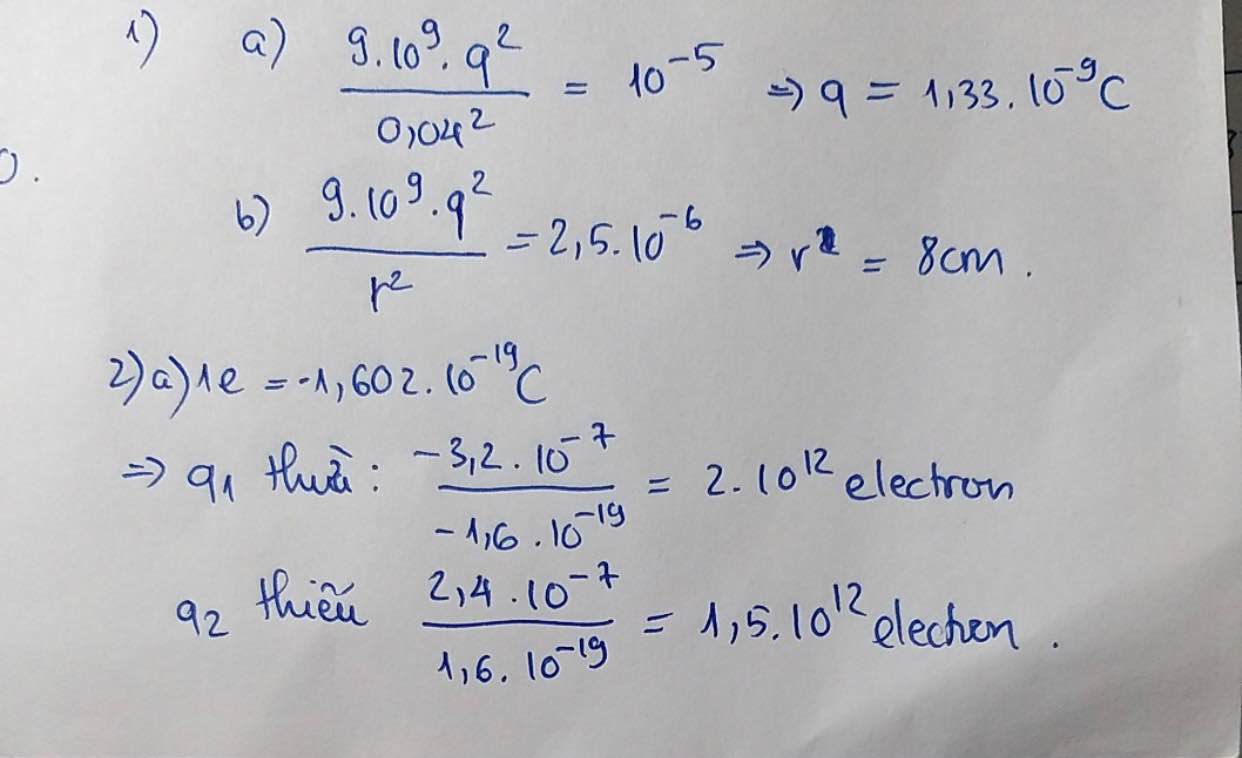

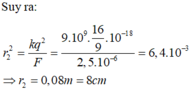
a) Độ lớn mỗi điện tích:
Ta có: F = k | q 1 q 2 | r 2 = k q 2 r 2 ⇒ |q| = r F k = 4 . 10 - 2 10 - 5 9 . 10 9 ≈ 1 , 3 . 10 - 9 (C).
b) Khoảng cách r ' = q k F ' = 1 , 3.10 − 9 9.10 9 2 , 5.10 − 6 = 7 , 8 . 10 - 2 m = 7,8