Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Độ lệch pha giữa M và N: Δ φ = 2 π d λ = 2 π d f v = 4 π 3
- Với câu A, ta có sơ đồ sau:
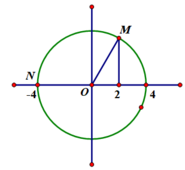
Từ đó vẽ được vị trí giữa M và N như sau:
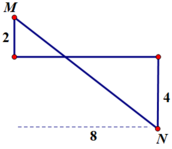
Dựa vào tam giác đồng dạng, tìm được MN = 10 cm => A sai.
- Với câu B, sơ đồ :
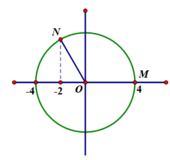
Khi đó xN = -2 (cm) suy ra v N = 3 2 A ω = 2 π 3 ( m / s ) . Lúc này N đang đi xuống => B sai.
- Với câu C :
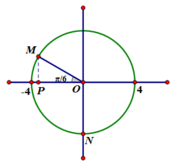
Có xM = OP = OM.cos 30 = 2 3 (cm). => C sai.
- Với câu D : để MN lớn nhất thì xM = xN. Ta có hình vẽ
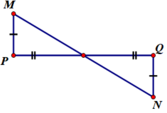
Từ đó tính được MN = 4 7 (cm) => D đúng

Đáp án D
Khi M ở vị trí cao nhất.
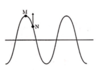
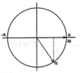
Theo chiều truyền của sóng từ trái qua phải các phần tử bên phải gần M đi lêN
Do M N < λ ; N có li độ dương bằng A 2 và đi lên nên sóng truyền từ M đến N
Từ hình: Dao động tại N chậm pha hơn tại M góc π 3
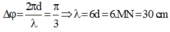
Tốc độ truyền sóng: ![]()

Đáp án D
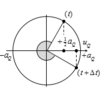
+ Khoảng cách từ vị trí cân bằng của một nút đến một bụng gần nhất là một phần tư lần bước sóng → λ = 24 cm → Chu kì của sóng T = λ v = 0 , 24 1 , 2 = 0 , 2 s.
Biên độ dao động một điểm trên dây cách nút gần nhất một đoạn d được xác định bởi biểu thức a = A sin 2 π d λ → a P = 2 2 a Q = 2 3 cm.
+ Ta chú ý rằng P và Q nằm trên hai bó sóng đối xứng nhau qua một bó nên dao động cùng pha, tại thời điểm t, thì u P = a P 2 = 2 cm thì u Q = a Q 2 = 3 cm và cũng đang hướng về vị trí cân bằng.
→ Từ hình vẽ, ta thấy khoảng thời gian tương ứng sẽ là Δ t = 3 T 4 = 0 , 015 s

Đáp án B
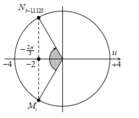
Ta có : λ = v f = 12 cm ⇒ MN = 37 cm = 3 λ + λ 12
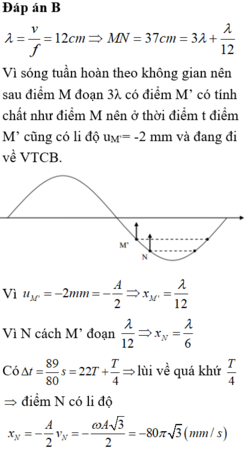
Vì sóng tuần hoàn theo không gian nên sau điểm M đoạn 3λ có điểm M’ có tính chất như điểm M nên ở thời điểm t điểm M’ cũng có li độ uM’= -2 mm và đang đi về VTCB.
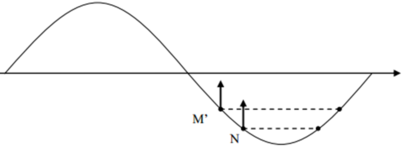
Vì uM’ = –2mm = –A/2 => xM’ = λ/12
Vì N cách M’ đoạn λ/12 => xN = λ/6.
Ta có : ∆ t = 89 80 s = 22 T + T 4 ⇒ lùi về quá khứ T 4
=> điểm N có li độ xN = –A/2
v N = - ωA 3 2 = - 80 π 3 ( mm / s ) .