Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

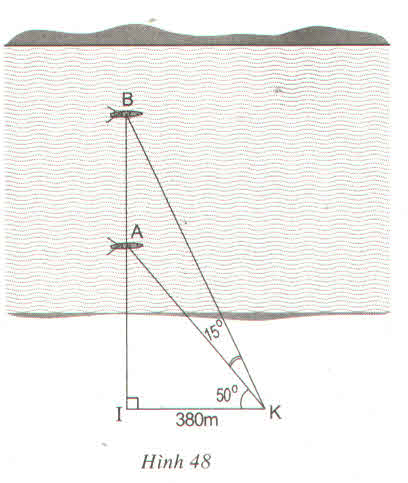
Trong tam giác vuông BIK có:
IB = IK.tg ∠IKB = IK.tg(50o + 15o) = 380.tg 65o ≈ 814 (m)
Trong tam giác vuông AIK có:
IA = IK.tg ∠IKA = IK.tg 50o = 380.tg50o ≈ 452 (m)
Vậy khoảng cách giữa hai thuyền là:
AB = IB – IA = 814 – 452 = 362 (m)

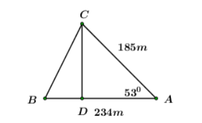
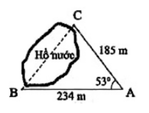
Từ C, dựng đường vuông góc với AB, cắt AB tại D.
Khi đó ta có: CD là đường cao của ABC.
Áp dụng tỉ số lượng giác của góc nhọn trong ACD vuông tại D ta có:
![]()
![]()
=> BD = AB – AD = 234 − 185. c o s 53 0
Áp dụng định lý Py-ta-go cho BCD để tính BC.
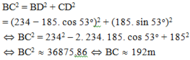
Đáp án cần chọn là: C

Lấy C sao cho C, A, B thẳng hàng. Đặt giác kế tại C và lấy D sao cho góc DCA = 90°.
– Chuyển giác kế sang D và đo góc CDA = α ; CDB = β
– Đo CD = m
Ta có : ∆CAD có góc C = 90°, góc D = α, CD = m nên CA = m.tgα .
ACDB có góc C = 90°, CD = m, góc D = β nên CB = CD.tgD = m.tgβ .
=> AB = CB – CA = m.tgβ – m.tgα = m(tgβ – tgα).
Tham khảo :

Gọi chân hải đăng là A thì ta để ý thấy. Lần đầu quan sát thì tam giác DAB là nửa tam giác đều
\(\Rightarrow DA^2+AB^2=DB^2\)
\(\Leftrightarrow DA^2+AB^2=4AB^2\)
\(\Leftrightarrow DA^2=3AB^2=3.75^2=11250\)
\(\Leftrightarrow DA=106,066\)
Lần thứ 2 quan sát thì tam giác CAB là tam giác vuông cân
\(\Rightarrow CA=AB=75\)
Vậy quãng đường thuyền đi được là:
\(DC=DA-CA=106,066-75=31,066\)

- Áp dụng tỉ số lượng giác vào tam giác ABC vuông tại B
\(\Rightarrow tan60=\dfrac{h}{BC}\)
\(\Rightarrow BC=\dfrac{h\sqrt{3}}{3}\)
\(\Rightarrow BD=BC+CD=\dfrac{h\sqrt{3}}{3}+600\)
- Áp dụng tỉ số lượng giác vào tam giác ABD vuông tại B
\(tan50=\dfrac{h}{BD}\)
\(\Rightarrow h=tan50.\left(\dfrac{h\sqrt{3}}{3}+600\right)\)
\(\Rightarrow h\approx2292m\)
Vậy ...
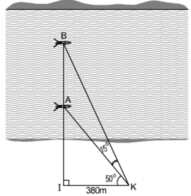
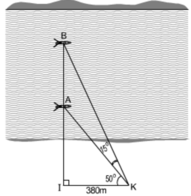

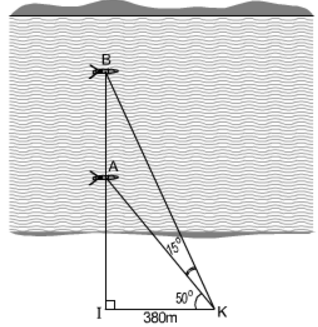
Trong tam giác vuông BIK có:
I B = I K . t g ∠ I K B = I K . t g ( 50 ° + 15 ° ) = 380 . t g 65 ° ≈ 814 ( m )
Trong tam giác vuông AIK có:
I A = I K . t g ∠ I K A = I K . t g 50 ° = 380 . t g 50 ° ≈ 452 ( m )
Vậy khoảng cách giữa hai thuyền là:
AB = IB – IA = 814 – 452 = 362 (m)