Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi thời gian vòi 1; vòi2 chảy 1 mình đẩy bể lần lượt là x;y(h)
đk: x,y>0
săng suất dự định của vòi 1 là : \(\frac{1}{x}\)(bể/h)
săng suất dự định của vòi2 là \(\frac{1}{y}\)(bể/h)
năng suất chảy chung của 2 vòi theo dự định là: \(\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}\) (bể/h)
thời gian 2 vòi chảy chung đầy bể là \(\frac{xy}{x+y}\)(h)
vì nếu 2vòi chat chung theo dự định sau 12h đầy bể nên ta có phương trình: \(\frac{xy}{x+y}\)=12\(\Leftrightarrow12x+12y=xy\)(1)
2 vòi chảy chung trong 8h được: \(8.\frac{x+y}{xy}=\frac{8x+8y}{xy}\) (bể )
năng suất thực tế của vòi 2 là 2/y(bể/h)
thực tế vòi 2 chảy rong 3h30'=7/2h được: \(\frac{7}{y}\) (bể)
vì thực tế 2 vòi đã chảy đầy bể nên ta có phương trình:
\(\frac{8x+8y}{xy}+\frac{7}{y}=1\) \(\Leftrightarrow15x+8y=xy\) (2)
từ (1) và (2) ta có hệ phương trình
\(\left\{{}\begin{matrix}15x+8y=xy\\12x+12y=xy\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=28\\y=21\end{matrix}\right.\) (tm)
thời gian vòi 1; vòi2 chảy 1 mình đẩy bể lần lượt là 28h;21h

Đáp án A
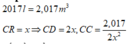
Số tiền để xây đáy là: ![]()
Số tiền để xây thân bể là: 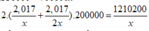
Số tiền để xây nắp bể là : ![]()
Số tiền để xây bể là :
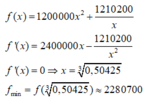

Chọn D
Sau khi chia tiền lần đầu tiên sẽ có 8 trường hợp xảy ra như sau:
| Raashan |
Sylvia |
Ted |
| 1 |
1 |
1 |
| 1 |
1 |
1 |
| 2 |
1 |
0 |
| 2 |
0 |
1 |
| 1 |
2 |
0 |
| 0 |
2 |
1 |
| 1 |
0 |
2 |
| 0 |
1 |
2 |
Các số lần lượt là số tiền của mỗi bạn. Có hai trường hợp cho kết quả (1;1;1) đó là Raashan → Sylvia → Ted Raashan hoặc Raashan Ted Sylvia Raashan.
Với mỗi trường hợp cho kết quả (1;1;1) thì lượt chơi tiếp theo sẽ có 1 4 cơ hội để số tiền mỗi người bằng nhau.
Đối với trường hợp một người có 2$, một người có 1$ và người còn lại không có tiền thì lượt chơi thứ hai sẽ có 4 trường hợp xảy ra. Không mất tính tổng quát ta giả sử Raashan có 2$, Sylvia có 1$ và Ted không có tiền, ta có những cách chuyển tiền như sau:
- Raashan ⇆ Sylvia và Ted không nhận được tiền.
Raashan → Sylvia → Ted.
- Raashan → Ted → Sylvia.
- Sylvia → Raashan → Ted.
Như vậy trong 4 khả năng trên chỉ có một khả năng cho kết quả (1;1;1) chiếm tỉ lệ 1 4
Cứ tiếp tục chơi như vậy đến lượt thứ 2019. Khi đó xác suất mỗi người chơi có 1$ là
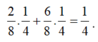

Gọi C là biến cố "Có ít nhất một người bắn trúng bia", khi đó biến cố đối của B là biến cố C
Do đó
P
(
C
)
=
1
−
P
(
B
)
=
1
−
0
,
06
=
0
,
94
.
Chọn đáp án C.




Bài toán này khá khó đấy, bạn phải chờ lâu chút
sao ko làm luôn đi