Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Số các số tự nhiên có hai chữ số phân biệt là 9.9 = 81 số.
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố “Hai chữ số được viết ra có ít nhất một chữ số chung”
Khi đó ta có biến cố A ¯ là “Hai chữ số được viết ra không có chữ số chung”
Gọi hai chữ số mà Công và Thành viết ra lần lượt là a b ¯ v à c d ¯
- TH1: b = 0, khi đó a có 9 cách, c có 8 cách và d có 7 cách. Vậy có 9.8.7 = 504 cách viết.
- TH2: b ≠ 0, khi đó a có 9 cách, b có 8 cách, c có 7 cách và d có 7 cách. Vậy có 9.8.7.7 = 3528 cách viết.
![]() cách viết.
cách viết.
Vậy xác suất của biến cố A là:
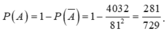
Nhận xét: Đây là một bài toán xác suất chọn số. Đối với bài toán này, ta sẽ đi theo hướng tính gián tiếp thông qua phần bù. Khi đó cách làm sẽ ngắn hơn và tránh nhầm lẫn không đáng có.

Chọn A
Xét phép thử: “Chọn ngẫu nhiên một số tự nhiên trong các số tự nhiên có bốn chữ số”
Ta có ![]()
Biến cố A: “Số được chọn có ít nhất hai chữ số 8 đứng liền nhau”.
Gọi số có 4 chữ số a b c d ¯ là trong đó có ít nhất hai chữ số 8 đứng liền nhau, a ≠ 0
TH1: Có đúng hai chữ số 8 đứng liền nhau.
+) Số có dạng 88 c d ¯ : có 9.9 = 81 số.
+) Số có dạng a 88 d ¯ hoặc a b 88 ¯ : mỗi dạng có 8.9 = 72 số.
TH2: Có đúng ba chữ số 8 trong đó có ít nhất hai chữ số 8 đứng liền nhau.
+) Số có dạng a 888 ¯ : có 8 số.
+) Số có dạng 8 b 88 ¯ hoặc 88 c 8 ¯ hoặc 888 d ¯ : Mỗi dạng có 9 số.
TH3: Cả 4 chữ số đều là chữ số 8: Có 1 số là số 8888
Do đó n(A) = 81 + 2.72 + 8 + 3.9 + 1 = 261
Xác suất cần tìm 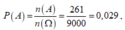

Chọn A
+ Số các chỉnh hợp chập của tập hợp các chữ số ![]()
Số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} mà chữ số 0 đứng vị trí đầu tiên ( 0 b c ¯ ) bằng số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} và bằng A 9 2 .
Suy ra số các số tự nhiên có chữ số đôi một khác nhau bằng ![]()
+ Lấy ngẫu nhiên ra từ hai số có ![]() cách.
cách.
+ Gọi là biến cố “lấy được từ hai số mà các chữ số có mặt ở hai số đó giống nhau”
Trường hợp 1: Ba chữ số có mặt trong hai số được lấy không có chữ số 0
Chọn ba chữ số trong tập {0;1;2;3;4;5;6;7;8;9} có C 9 3 cách.
Ba chữ số này tạo thành 3! = 6 số trong A.
Lấy hai số trong 6 số này có C 6 2 cách (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có C 9 3 . C 6 2 cách lấy hai số thỏa trường hợp 1.
Trường hợp 2: Ba chữ số có mặt trong hai số được lấy có chữ số .
Chọn thêm hai chữ số trong tập {0;1;2;3;4;5;6;7;8;9}có C 9 2 cách.
Ba chữ số này (hai chữ số vừa chọn và chữ số 0) tạo thành 2.2! = 4 số trong A.
Lấy hai số trong 4 số này có C 4 2 (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có C 9 2 . C 4 2 cách lấy hai số thỏa trường hợp 2.
Suy ra ![]()
+ Do đó, xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau là:
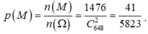

Không gian mẫu: \(9.10.10.10=9000\)
Số cách viết thỏa mãn: \(C_{10}^4=210\)
Xác suất: \(P=\dfrac{210}{9000}=...\)

Chọn A
Vì là tập tất cả các số tự nhiên có 5 chữ số nên
![]()
![]()
![]()
Số phần tử của không gian mẫu là ![]()
Gọi X là biến cố: “Chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1 từ tập A”.
![]() có tận cùng bằng 1,do đó
có tận cùng bằng 1,do đó ![]() với
với ![]() có chữ số tận cùng là 3.
có chữ số tận cùng là 3.
Xét các trường hợp sau:
1) M là số có 4 chữ số có dạng
m
n
p
q
¯
Khi đó: ![]()
- Với m = 1, do ![]() và q = 3 nên n
≥
4
và q = 3 nên n
≥
4
+) Khi n = 4 thì p > 2 nên p ∈ {4;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi n ≥ 5: Có 5 cách chọn n thuộc tập hợp {5;6;7;8;9}. Khi đó p ≠ m,n,q nên p có 7 cách chọn. Ta được 35 số thỏa mãn.
- Với m
≥
2 tức là có 7 cách chọn m từ tập {2;4;5;6;7;8;9}. Khi đó ![]() với mọi n,p thuộc tập hợp {0;1;2;4;5;6;7;8;9} và n
≠
p
≠
m, do đó có 8 cách chọn n, có 7 cách chọn p. Ta được 7.8.7 = 392 số thỏa mãn
với mọi n,p thuộc tập hợp {0;1;2;4;5;6;7;8;9} và n
≠
p
≠
m, do đó có 8 cách chọn n, có 7 cách chọn p. Ta được 7.8.7 = 392 số thỏa mãn
2) M là số có 5 chữ số có dạng m n p q r ¯ Khi đó: m n p q r ¯ ≤ 14285 và r = 3
Do m n p q r ¯ ≤ 14285 nên m chỉ nhận giá trị bằng 1 và n ≤ 4
- Với m=1; n = 0,2 thì p,q là các số tùy ý thuộc tập {0;2;4;5;6;7;8;9} và p ≠ q ≠ n Ta được 2.7.6 = 84 số thỏa mãn.
- Với m=1; n = 4:
+) Khi p = 0 thì q là số tùy ý thuộc tập {2;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi p = 2 thì q phải thuộc tập {0;5;6;7;8}. Ta được 5 số thỏa mãn.
Vậy số phần tử của biến cố X là n(X) = 6 + 35 + 392 + 84 + 6 + 5 = 528
Xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là 1 bằng
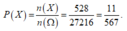

Đáp án D
Có 6 cặp số có tổng lớn hơn 7 là (5;3); (5;4); (6;2); (6;3); (6;4); (6;5) nên ứng với 12 số có hai chữ số khác nhau mà có tổng lớn hơn 7.
Mặt khác, số các số có hai chữ số khác nhau được lập từ các chữ số 1; 2; 3; 4; 5; 6 là ![]() = 30 số.
= 30 số.
Do đó, xác suất là:
![]()



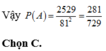
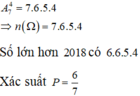


Chọn C
Cách 1: Số các số tự nhiên có hai chữ số phân biệt là 9.9 = 81 số.
Số phần tử của không gian mẫu là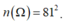
Gọi A là biến cố thỏa mãn bài toán.
+ Khả năng 1: Hai bạn chọn số giống nhau nên có 81 cách.
+ Khả năng 2: Hai bạn chọn số đảo ngược của nhau nên có 9.8 = 72 cách.
+ Khả năng 3: Hai bạn chọn số chỉ có một chữ số trùng nhau
- TH1: Trùng chữ số 0: Công có 9 cách chọn số và Thành đều có 8 cách chọn số nên có 9.8 = 72 cách.
- TH 2: Trùng chữ số 1: Nếu Công chọn số 10 thì Thành có 16 cách chọn số có cùng chữ số 1. Nếu Công chọn số khác 10, khi đó Công có 16 cách chọn số và Thành có 15 cách chọn số có cùng chữ số 1 với Công nên có 16 + 16.15 = 16.16 256 cách.
- Các trường hợp chọn trùng chữ số 2,3,4,....,9 tương tự.
Vậy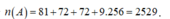
Xác suất cần tính là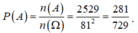
Cách 2: Số các số tự nhiên có hai chữ số phân biệt là 9.9= 81 số.
Số phần tử của không gian mẫu là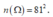
Gọi là biến cố thỏa mãn bài toán. Xét biến cố A ¯
- TH 1: Công chọn số có dạng a 0 ¯ nên có 9 cách. Khi đó có 25 số có ít nhất một chữ số trùng với số a 0 ¯ nên Thành có 81 - 25 = 56 cách chọn số không có chữ số trùng với Công. Vậy có 9.56 = 504 cách.
- TH 2: Công chọn số không có dạng a 0 ¯ : Có 72 cách, khi đó 32 số có ít nhất một chữ số trùng với số của Công chọn nên Thành có 81 - 32 = 49 cách chọn số không có chữ số nào trùng với Thành. Vậy có 72.49 = 3528 cách.