K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
29 tháng 9 2017
Đáp án A
Phương pháp.
Giả sử ![]() Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa ![]() về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm 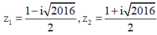
Giả sử ![]() . Từ
. Từ ![]() ta suy ra
ta suy ra
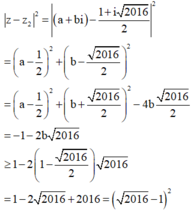
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của ![]() là
2016
-
1
là
2016
-
1
Đạt được khi và chỉ khi ![]()

CM
16 tháng 3 2019
Đáp án A
Phương trình 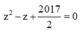
![]()
![]()
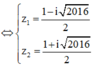
Ta có ![]()
![]()
![]()
Vật giá trị nhỏ nhất của biểu thức P là ![]()
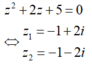
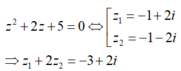
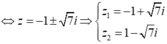



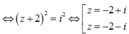
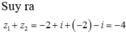
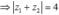
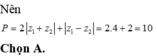
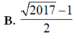
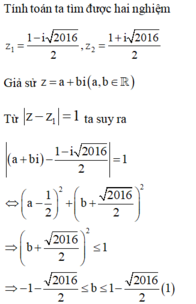

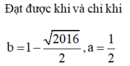
Lời giải:
Theo đề thì $z_1=2+i, z_2=2-i$. Khi đó:
$A=(z_1-1)^{2021}+(z_2-1)^{2022}=(i+1)^{2021}+(1-i)^{2022}$
Ta có:
$(i+1)^2=i^2+1+2i=(-1)+1+2i$
$(1-i)^2=1+i^2-2i=-2i$
$\Rightarrow A=(2i)^{1010}(i+1)+(-2i)^{1011}$
$=2^{1010}.(i^2)^{505}(i+1)+(-2)^{1011}.(i^2)^{505}.i$
$=2^{1010}.(-1)^{505}(i+1)+(-2)^{1011}.(-1)^{505}i$
$=-(i+1).2^{1010}+2^{1011}i$
$=2^{1010}(i-1)$