ngày THI ĐẤU OLM tối nay, ngày 28/04/2023 để so tài với học sinh toàn quốc!!!

Ôn tập kiểm tra học kì 2 hiệu quả, đạt thành tích cao!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
11 tháng 8 2017
Gọi S là tập nghiệm của phương trình  2 log 2 2 x − 2 + log 2 x − 3 2 = 2  trên  ℝ .  Tổng các phần tử của S là: A. 8 +  2 B. 4 +  2 C. 6 +  2 D....
Đọc tiếp

Gọi S là tập nghiệm của phương trình  2 log 2 2 x − 2 + log 2 x − 3 2 = 2  trên  ℝ .  Tổng các phần tử của S là:

A. 8 +  2

B. 4 +  2

C. 6 +  2

D. 8
#Mẫu giáo
1
CM
Cao Minh Tâm
11 tháng 8 2017

Đáp án B

Đúng(0)
PT
Pham Trong Bach
9 tháng 3 2019

Gọi S là tập nghiệm của phương trình 2 l o g 2 ( 2 x - 2 ) + l o g 2 ( x - 3 ) 2 = 2 . Tổng các phần tử của S bằng:

A. 6

B.  4 + 2

C.  2 + 2

D.  8 + 2

#Mẫu giáo
1
CM
Cao Minh Tâm
9 tháng 3 2019

Chọn B

Đúng(0)
PT
Pham Trong Bach
30 tháng 12 2018

Gọi S là tập nghiệm của phương trình 2 log 2 2 x − 2 + log 2 x − 3 2 = 2  trên R. Tổng các phần tử của S bằng

A. 8

B.  4 + 2

C.  8 + 2

D.  6 + 2

#Mẫu giáo
1
CM
Cao Minh Tâm
30 tháng 12 2018

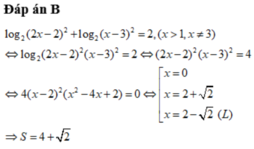
Đáp án B

Phương pháp:

- Tìm điều kiện xác định.

- Biến đổi phương trình về dạng cơ bản  log a f x = m ⇔ f x = a m

Cách giải:

Điều kiện:  x > 1 ;   x ≠ 3

Đúng(0)
PT
Pham Trong Bach
8 tháng 2 2018
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2  có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘  bằng: A. 150. B. 100. C. 30....
Đọc tiếp

Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2  có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘  bằng:

A. 150.

B. 100.

C. 30.

D. 50.
#Mẫu giáo
1
CM
Cao Minh Tâm
8 tháng 2 2018

Đáp án D

Đúng(0)
PT
Pham Trong Bach
23 tháng 10 2017
Tích các nghiệm của phương trình  log 2   x + 2 - log   x = 2  là A.  10 3 - 5 2 B.  10 3 + 2 2 C.  10 3 + 5 2 D.  10 3 - 2 2 ...
Đọc tiếp

Tích các nghiệm của phương trình  log 2   x + 2 - log   x = 2  là

A.  10 3 - 5 2

B.  10 3 + 2 2

C.  10 3 + 5 2

D.  10 3 - 2 2

#Mẫu giáo
1
CM
Cao Minh Tâm
23 tháng 10 2017

Đáp án đúng : A

Đúng(0)
PT
Pham Trong Bach
4 tháng 12 2017
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2  có dạng S = (a;b)\{x0}. Giá trị của a + b – x0  bằng: A. 100 B. 30 C. 150 D....
Đọc tiếp

Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2  có dạng S = (a;b)\{x0}. Giá trị của a + b – x0  bằng:

A. 100

B. 30

C. 150

D. 50
#Mẫu giáo
1
CM
Cao Minh Tâm
4 tháng 12 2017

Đáp án D.

Phương pháp: 

Cách giải: ĐK: 

Đúng(0)
PT
Pham Trong Bach
30 tháng 3 2017
Gọi S là tập tất cả các giá trị thực của tham số m để bất phương trình x 6 + 3 x 4 − m 3 x 3 + 4 x 2 − m x + 2 ≥ 0  có nghiệm  với  mọi x ∈ ℝ .  Biết  rằng S = a ; b , a , b ∈ ℝ .  Tính  P = 2 b − 3 a A. P = 5 B. P = 10 C. P = 15 D. P =...
Đọc tiếp

Gọi S là tập tất cả các giá trị thực của tham số m để bất phương trình

x 6 + 3 x 4 − m 3 x 3 + 4 x 2 − m x + 2 ≥ 0  có nghiệm  với  mọi x ∈ ℝ .  Biết  rằng S = a ; b , a , b ∈ ℝ .  Tính  P = 2 b − 3 a

A. P = 5

B. P = 10

C. P = 15

D. P = 0
#Mẫu giáo
1
CM
Cao Minh Tâm
30 tháng 3 2017

Chọn B

Đúng(0)
PT
Pham Trong Bach
13 tháng 9 2018
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2  (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . ...
Đọc tiếp

Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2  (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức

log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n   c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0  (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/

A. 0

B. 1

C. 2

D. Vô số
#Mẫu giáo
1
CM
Cao Minh Tâm
13 tháng 9 2018

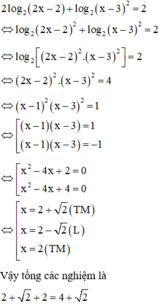
Chọn B

Cách giải: Ta có:

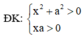
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n   c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0

Đúng(0)
PT
Pham Trong Bach
10 tháng 9 2017
Gọi S là tập nghiệm của phương trình 2 − x 2 + 4 x = 6.  Khi đó, số phần tử của tập S là A. S = 2 B. S = 3 C. S = 4 D. S = 5 ...
Đọc tiếp

Gọi S là tập nghiệm của phương trình 2 − x 2 + 4 x = 6.  Khi đó, số phần tử của tập S là

A. S = 2

B. S = 3

C. S = 4

D. S = 5

#Mẫu giáo
1
CM
Cao Minh Tâm
10 tháng 9 2017

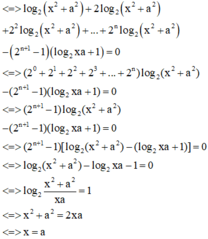
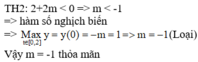
Đáp án  B

Xét hàm số f x = 4 x + 2 2 − x − 6  với x ∈ ℝ ,  có f ' x = 4 x 2 ln 4 − 1 − x ln 4  

Suy ra f ' ' x = 4 x 2 ln 2 4 − 2 ln 4 − x ln 2 4 ; f ' ' x = 0 ⇔ x = 2 ln 4 − 2 ln 4 .  

Do đó f ' x = 0  có không quá 2 nghiệm f ' x = 0  có không quá 3 nghiệm.

Mà f 0 = 0 ; f 1 2 = 0 ; f 1 = 0 ⇒ x = 0 ; 1 2 ; 1  là 3 nghiệm của phương trình.

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP