Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Đồ thị hàm số y = x 3 - 3 x + 1 là đồ thị bên dưới
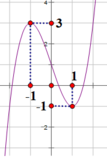
Từ đồ thị hàm số y = x 3 - 3 x + 1 suy ra đồ thị hàm số y = x 3 - 3 x + 1 là đồ thị bên dưới
Dựa vào đồ thị hàm số y = x 3 - 3 x + 1 và đồ thị hàm số y = 2 m - 1
Ta có: đường thẳng y = 2 m - 1 cắt đồ thị hàm số y = x 3 - 3 x + 1 tại 4 điểm phân biệt
⇔ - 1 < 2 m - 1 < 1 ⇔ 0 < m < 1

Ta có y ' = 3 x 2 - 4 x + 2
Do tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2016 nên hệ số góc của tiếp tuyến là k = 1
Chọn A

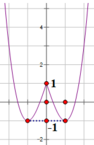
Phương trình hoành độ giao điểm: \(x^4-5x^2-m+4=0\)
Đặt \(x^2=t\Rightarrow t^2-5t-m+4=0\) (1)
Gọi 4 hoành độ giao điểm là \(x_1< x_2< x_3< x_4\) và \(t_1< t_2\) là 2 nghiệm dương phân biệt của (1) thì: \(\left\{{}\begin{matrix}x_1=-\sqrt{t_2}\\x_2=-\sqrt{t_1}\\x_3=\sqrt{t_1}\\x_4=-\sqrt{t_2}\end{matrix}\right.\)
Do 4 điểm cách đều \(\Rightarrow x_2-x_1=x_3-x_2\Rightarrow x_1+x_3=2x_2\)
\(\Rightarrow-\sqrt{t_2}+\sqrt{t_1}=-2\sqrt{t_1}\) \(\Rightarrow3\sqrt{t_1}=\sqrt{t_2}\Rightarrow t_2=9t_1\)
\(\Rightarrow\left\{{}\begin{matrix}t_1+t_2=5\\t_2=9t_1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}t_1=\dfrac{1}{2}\\t_2=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow-m+4=t_1t_2=\dfrac{9}{4}\)
\(\Rightarrow m=\dfrac{7}{4}\)

Giao điểm với trục tung B(0 ;-1). Ta có
Hệ số góc của tiếp tuyến của đồ thị hàm số 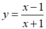 tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
Chọn B

Chọn C
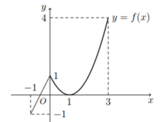
Quan sát đồ thị ta thấy hàm số y = f(x) đạt giá trị nhỏ nhất trên [-1;3] là -1 tại điểm x = =-1 và đạt giá trị lớn nhất trên[-1;3] là 4 tại điểm x = 3. Do đó M = 4, m = -1.
Giá trị M - m = 4 - (-1) = 5.

* Nếu m = 0 thì y = x nên hàm số đã cho không có tiệm cận ngang.
* Nếu m = 1 thì y = 1 nên hàm số không có tiệm cận ngang.
* Nếu m = -1 thì y = -1 nên hàm số không có tiệm cận ngang.

Vậy để hàm số đã cho có tiệm cận ngang thì m ≠ 0 và m ≠ ±1;
Chọn D
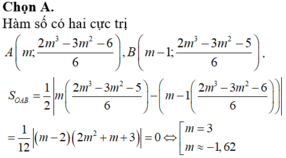
Chọn A