Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi k là cặp số thực(x,y) #0 thỏa mãn :
\(\left(x^2+1\right)\left(x^2+y^2\right)-4x^2y=0\), vậy k=...


x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1 ⇔ ( 1 + x ) 2 ( 1 + y ) 2 = 1 − x y ⇒ ( 1 + x 2 ) ( 1 + y 2 ) = 1 - x y 2 ⇔ 1 + x 2 + y 2 + x 2 y 2 = 1 − 2 x y + x 2 y 2 ⇔ x 2 + y 2 + 2 x y = 0 ⇔ x + y 2 = 0 ⇔ y = − x ⇒ x 1 + y 2 + y 1 + x 2 = x 1 + x 2 − x 1 + x 2 = 0

Lời giải:
Để pt có 2 nghiệm $x_1,x_2$ thì: $\Delta=k^2-8\geq 0$
$\Leftrightarrow k^2\geq 8(1)$
Áp dụng định lý Viet:
$x_1+x_2=-k$
$x_1x_2=2$
Khi đó:
$(\frac{x_1}{x_2})^2+(\frac{x_2}{x_1})^2> 23$
$\Leftrightarrow \frac{x_1^4+x_2^4}{(x_1x_2)^2}>23$
$\Leftrightarrow x_1^4+x_2^4> 23(x_1x_2)^2=23.2^2=92$
$\Leftrightarrow (x_1^2+x_2^2)^2-2(x_1x_2)^2> 92$
$\Leftrightarrow (x_1^2+x_2^2)^2-8> 92$
$\Leftrightarrow [(x_1+x_2)^2-2x_1x_2]^2>100$
$\Leftrightarrow (k^2-4)^2>100$
$\Leftrightarrow k^2-4>10$ hoặc $k^2-4<-10$
$\Leftrightarrow k^2>14$ hoặc $k^2<-6$ (loại)
$\Leftrightarrow k> \sqrt{14}$ hoặc $k< -\sqrt{14}$
Kết hợp với $k^2\geq 8$ suy ra $k> \sqrt{14}$ hoặc $k< -\sqrt{14}$


Ta có (1) ⇔ x 4 + x 2 + 20 = y 2 + y
Ta thấy: x 4 + x 2 < x 4 + x 2 + 20 ≤ x 4 + x 2 + 20 + 8 x 2 ⇔ x 2 ( x 2 + 1 ) < y ( y + 1 ) ≤ ( x 2 + 4 ) ( x 2 + 5 )
Vì x, y ∈ Z nên ta xét các trường hợp sau
+ TH1. y ( y + 1 ) = ( x 2 + 1 ) ( x 2 + 2 ) ⇔ x 4 + x 2 + 20 = x 4 + 3 x 2 + 2 ⇔ 2 x 2 = 18 ⇔ x 2 = 9 ⇔ x = ± 3
Với x 2 = 9 ⇒ y 2 + y = 9 2 + 9 + 20 ⇔ y 2 + y − 110 = 0 ⇔ y = 10 ; y = − 11 ( t . m )
+ TH2 y ( y + 1 ) = ( x 2 + 2 ) ( x 2 + 3 ) ⇔ x 4 + x 2 + 20 = x 4 + 5 x 2 + 6 ⇔ 4 x 2 = 14 ⇔ x 2 = 7 2 ( l o ạ i )
+ TH3: y ( y + 1 ) = ( x 2 + 3 ) ( x 2 + 4 ) ⇔ 6 x 2 = 8 ⇔ x 2 = 4 3 ( l o ạ i )
+ TH4: y ( y + 1 ) = ( x 2 + 4 ) ( x 2 + 5 ) ⇔ 8 x 2 = 0 ⇔ x 2 = 0 ⇔ x = 0
Với x 2 = 0 ta có y 2 + y = 20 ⇔ y 2 + y − 20 = 0 ⇔ y = − 5 ; y = 4
Vậy PT đã cho có nghiệm nguyên (x;y) là :
(3;10), (3;-11), (-3; 10), (-3;-11), (0; -5), (0;4).


Xét pt :
\(x^2-2\left(k+2\right)x+k^2+2k-7=0\)
\(\Delta'=\left(k+2\right)^2-\left(k^2+2k-7\right)\)
\(=k^2+4k+4-k^2-2k+7\)
\(=2k+11\)
Để phương trình có 2 nghiệm pb \(\Leftrightarrow k>-\dfrac{11}{2}\)
Theo định lí Viet ta có :
\(\left\{{}\begin{matrix}x_1+x_2=2\left(k+2\right)\\x_1.x_2=k^2+2k-7\end{matrix}\right.\)
Ta có :
\(x_1^2+x_2^2=x_1.x_2+28\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=3x_1.x_2+28\)
\(\Leftrightarrow4\left(k+2\right)^2=3\left(k^2+2k-7\right)+28\)
Tự giải hết pt tìm k nhé :> Buồn ngủ quá ~
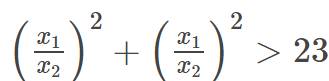
mk đưa lun kết quả : k = 2..check mk nhá
pt<=> x^4+y^2+x^2*y^2+x^2-4x^2y=0
=>(x^4-2x^2y+y^2)+x^2(1-2y+y^2)=0