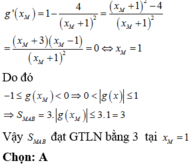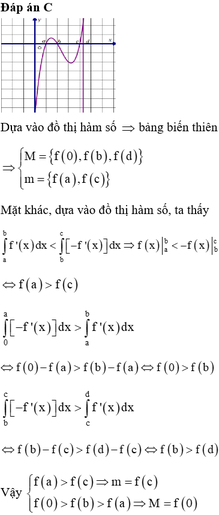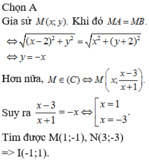Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
- Gọi tọa độ điểm M thuộc đồ thị hàm số.
- Tính khoảng cách từ M đến AB suy ra diện tích.
- Từ đó sử dụng phương pháp hàm số tìm GTLN của diện tích tam giác ABM.
Cách giải:

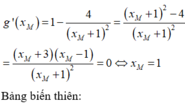

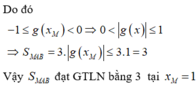

Đáp án C
Ta có: h ' x = f ' x − g ' x = 0 ⇔ x = a x = b x = c
Với x ∈ a ; b thì đồ thị g ' x nằm trên f ' x nên g ' x > f ' x ⇒ h ' x < 0 hàm số nghịch biến trên đoạn a ; b
Tương tự với x ∈ b ; c thì h x đồng biến.
Do đó M i n a ; c h x = h b .

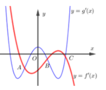
Đáp án A
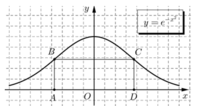
Theo hình vẽ , gọi D t ; 0 , A − t ; 0 và C t ; e − t 2 , B − t ; e − t 2 với t>0
Suy ra A B ¯ = 0 ; e − t 2 ⇒ A B = e − t 2 và B C = 2 t → S A B C D = A B . B C = 2 t . e − t 2
Xét hàm số f t = t e t 2 trên khoảng 0 ; + ∞ , có f ' t = 1 − 2 t 2 e − t 2
Do đó, giá trị lớn nhất của hàm số f t là max 0 ; + ∞ f t = 1 2 e . Vậy S max = 2 e

Đáp án C
- Viết phương trình tiếp tuyến với C tại M.
+ Phương trình tiếp tuyến với đồ thị hàm số y = f x tại điểm M x 0 ; f x 0 :y=f ' x o x-x o +f x o .
- Tìm tọa độ hai giao điểm A,B của tiếp tuyến với các trục tọa độ Ox, Oy.
- Diện tích tam giác OAB là: S Δ O A B = 1 2 O A . O B .
y = 1 x ⇒ y ' = 1 x 2 . Ta có:
x M = 2 − 3 ⇒ y M = 1 2 − 3 = 2 + 3 ⇒ M 2- 3 ; 2 + 3 .
Phương trình tiếp tuyến với C tại M 2- 3 ; 2 + 3 là:
d : y = − y ' x M x-x M + y M = − 1 2 − 3 2 x − 2 + 3 + 2 + 3 = − 2 + 3 2 x + 4 + 2 3 .
Cho x = 0 ⇒ y = 4 + 2 3 ⇒ B 0;4+2 3
Cho
y = 0 ⇒ x = 4 + 2 3 2 + 3 = 2 2 + 3 = 4 − 2 3 ⇒ A 4 − 2 3 ; 0
Vậy S O A B = 1 2 O A . O B = 1 2 4 + 2 3 4 − 2 3 = 2 .