Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Từ
f x . f ' x = 2 x f 2 x + 1 ⇒ f x . f ' x f 2 x + 1 = 2 x ⇒ ∫ f x . f ' x f 2 x + 1 d x = ∫ 2 x d x
(1)
Đặt
f 2 x + 1 = t ⇒ f 2 x = t 2 − 1 ⇒ 2 f x . f ' x d x = 2 t d t ⇒ f x . f ' x d x = t d t
Suy ra ∫ f x . f ' x f 2 x + 1 x = ∫ t d t t = ∫ d t = t + C 1 = f 2 x + 1 + C 1 và ∫ 2 x d x = x 2 + C 2
Từ (1) ta suy ra f 2 x + 1 + C 1 = x 2 + C 2 . Do f 0 = 0 nên C 2 − C 1 = 1 .
Như vậy
f 2 x + 1 = x 2 + C 2 − C 1 = x 2 + 1 ⇒ f 2 x = x 2 + 1 2 − 1 = x 4 + 2 x 2
⇒ f x = x 4 + 2 x 2 = x x 2 + 2 = x x 2 + 2
(do x ∈ 1 ; 3 ).
Ta có f ' x = x 2 + 2 + x 2 x 2 + 2 = 2 x 2 + 1 x 2 + 2 > 0, ∀ x ∈ ℝ ⇒ Hàm số f x = x x 2 + 2 đồng biến trên R nên f x cũng đồng biến trên 1 ; 3 .
Khi đó M = max 1 ; 3 f x = f 3 = 3 11 và m = min 1 ; 3 f x = f 1 = 3 .
Vậy
P = 2 M − m = 6 11 − 3 ⇒ a = 6 ; b = 1 ; c = 0 ⇒ a + b + c = 7

Đáp án A
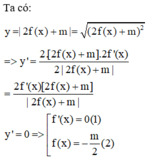
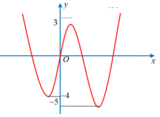
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy
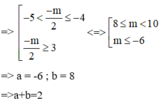

Đáp án D.
Phương pháp
Phương pháp tìm GTLN, GTNN của hàm số y = f x trên [ a ; b ] .
+) Giải phương trình y ' = 0 ⇒ các nghiệm x i ∈ a ; b
+) Tính các giá trị f a ; f b ; f x i
+) So sánh và kết luận:
max a ; b f x = max f a ; f b ; f x i ; min a ; b f x = min f a ; f b ; f x i
Cách giải
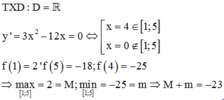
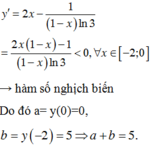
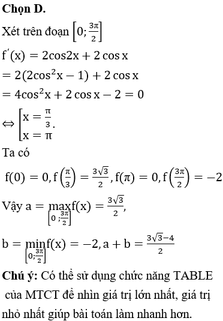

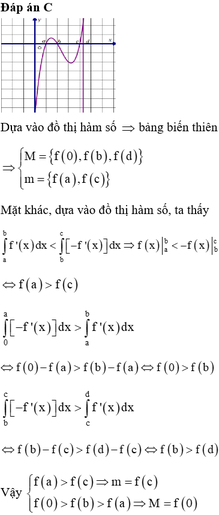
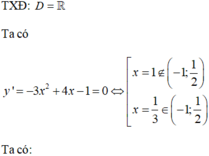
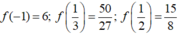
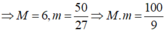
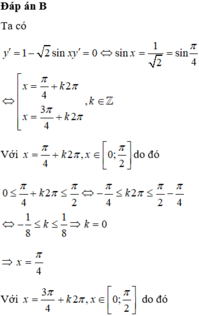
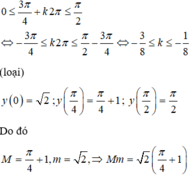

Chọn đáp án C.