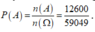Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(n_{\Omega}=A_8^5-A_7^4=5880\)
Chọn 3 chữ số chẵn: \(C_4^3=4\) cách
Chọn 2 chữ số lẻ: \(C_4^2=6\) cách
Xếp 2 số lẻ liền nhau, sau đó hoán vị với 3 chữ số chẵn: \(2!.4!=48\) cách
Chọn 3 chữ số chẵn sao cho có mặt chữ số 0: \(C_3^2=3\) cách
Hoán vị 5 chữ số sao cho 2 số lẻ liền nhau và số 0 đứng đầu: \(2!.3!=12\) cách
\(\Rightarrow6.\left(4.48-3.12\right)=936\)
Xác suất: \(P=\dfrac{936}{5880}=\dfrac{39}{245}\)

Không gian mẫu: \(A_9^5\)
Gọi số cần lập có dạng \(\overline{abcde}\)
\(\Rightarrow e\) có 4 cách chọn
Chọn bộ abcd:
- Chọn 2 số lẻ từ 5 số lẻ và hoán vị chúng: \(A_5^2\) cách
- Chọn 2 số chẵn từ 3 số chẵn còn lại (khác e): \(C_3^2\) cách
\(\Rightarrow\) Bộ abcd có \(A_5^2.C_3^2.3!\) cách
Xác suất: \(P=\dfrac{4.A_5^2.C_3^2.3!}{A_9^4}=...\)

Chọn D
Không gian mẫu được mô tả là Ω : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: ![]()
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là C 9 3 . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả 3 . 5 ! 5 số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: 3 . 5 ! 2 ! . 2 ! số tự nhiên.
Suy ra số phần tử của biến cố A là: ![]()
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: