Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Với \(m=3\) pt trở thành: \(2x^2+5x+2=0\)
\(\Delta=5^2-4.2.2=9>0\) nên pt có 2 nghiệm phân biệt:
\(x_1=\dfrac{-5+\sqrt{9}}{2.2}=-\dfrac{1}{2}\)
\(x_2=\dfrac{-5-\sqrt{9}}{2.2}=-2\)
b.
\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0;\forall m\)
Phương trình luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m-1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
\(4x_1^2+2x_1x_2+4x_2^2=1\)
\(\Leftrightarrow4\left(x_1^2+2x_1x_2+x_2^2\right)-6x_1x_2=1\)
\(\Leftrightarrow4\left(x_1+x_2\right)^2-6x_1x_2=1\)
\(\Leftrightarrow\left(2m-1\right)^2-3\left(m-1\right)=1\)
\(\Leftrightarrow4m^2-7m+3=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{3}{4}\end{matrix}\right.\)


Gọi thời gian làm 1 mình xong công việc của người thứ nhất là x giờ (x>0)
Thời gian làm 1 mình xong công việc của người 2 là y giờ (y>0)
Trong 1h người thứ nhất làm 1 mình được \(\dfrac{1}{x}\) phần công việc, người 2 làm 1 mình được \(\dfrac{1}{y}\) phần công việc
Do 2 người cùng làm trong 18h thì xong nên:
\(18\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\)
Người thứ nhất làm 4h được: \(\dfrac{4}{x}\) phần công việc
Người thứ 2 làm trong 7h được: \(\dfrac{7}{y}\) phần công việc
Do... trong 7h được 1/3 công việc nên: \(\dfrac{4}{x}+\dfrac{7}{y}=\dfrac{1}{3}\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{4}{x}+\dfrac{7}{y}=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{54}\\\dfrac{1}{y}=\dfrac{1}{27}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=54\\y=27\end{matrix}\right.\)

a: Thay x=2 và y=0 vào (d), ta được:
-n+3+4=0
=>1-n=0
hay n=1
b: Phương trình hoành độ giao điểm là:
\(x^2-2x+n-3=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot\left(n-3\right)=-4n+12+4=-4n+16\)
Để phương trình có hai nghiệm phân biệt thì -4n+16>0
hay n<4

a: \(=\dfrac{\sqrt{3}\left(x\sqrt{2}+y\sqrt{5}\right)}{2\left(x\sqrt{2}+y\sqrt{5}\right)}=\dfrac{\sqrt{3}}{2}\)
b: \(=\dfrac{a+\sqrt{a}-a-2}{\sqrt{a}+1}:\dfrac{a-\sqrt{a}+\sqrt{a}-4}{a-1}\)
\(=\dfrac{\left(\sqrt{a}-2\right)}{\sqrt{a}+1}\cdot\dfrac{a-1}{a-4}=\dfrac{\sqrt{a}-1}{\sqrt{a}+2}\)

a.
Với \(m=-1\) pt trở thành: \(x^2+4x-2=0\)
\(\Delta'=4+2=6>0\) nên pt có 2 nghiệm pb:
\(x_1=-2+\sqrt{6}\) ; \(x_2=-2-\sqrt{6}\)
b.
\(\Delta'=\left(m-1\right)^2-\left(m^2-3\right)=-2m+4\ge0\Rightarrow m\le2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3\end{matrix}\right.\)
\(x_1\left(x_1-x_2\right)+x_2^2=33\)
\(\Leftrightarrow x_1^2+x_2^2-x_1x_2=33\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=33\)
\(\Leftrightarrow4\left(m-1\right)^2-3\left(m^2-3\right)=33\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10>2\left(loại\right)\\m=-2\end{matrix}\right.\)

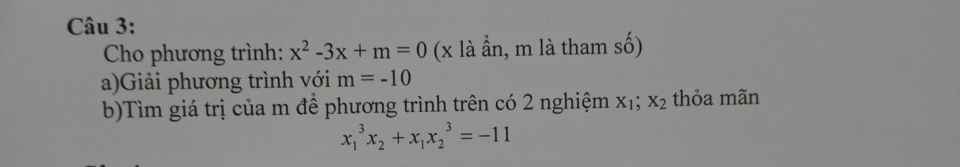





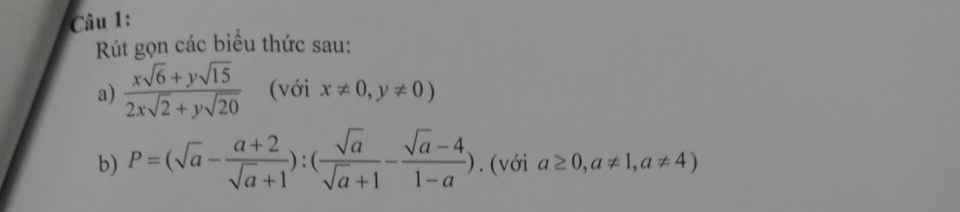
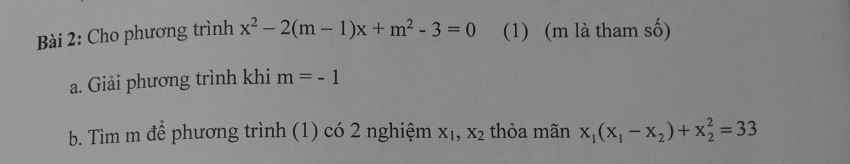


a)\(x^2+3x-10=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)