
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



-13/25x9/17+13/17x8/25+(-13/25)
=-13/25x9/17+8/17x13/25+(-13/25)
=13x(-9/17+8/17-1)
=13x(-18/17)=-234
a) Ta có: \(\dfrac{-13}{25}\cdot\dfrac{9}{17}+\dfrac{13}{17}\cdot\dfrac{8}{25}+\dfrac{-13}{25}\)
\(=\dfrac{-13}{25}\cdot\dfrac{9}{17}-\dfrac{-13}{25}\cdot\dfrac{8}{17}+\dfrac{-13}{25}\)
\(=\dfrac{-13}{25}\left(\dfrac{9}{17}-\dfrac{8}{17}+1\right)\)
\(=\dfrac{-13}{25}\cdot\dfrac{18}{17}\)
\(=-\dfrac{234}{425}\)

Sửa đề: \(\dfrac{1}{1.9}\rightarrow\dfrac{9}{9.19}\)
Giải:
\(N=\dfrac{9}{9.19}+\dfrac{9}{19.29}+\dfrac{9}{29.39}+...+\dfrac{9}{2019.2029}\)
\(N=\dfrac{9}{10}.\left(\dfrac{10}{9.19}+\dfrac{10}{19.29}+\dfrac{10}{29.39}+...+\dfrac{10}{2019.2029}\right)\)
\(N=\dfrac{9}{10}.\left(\dfrac{1}{9}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{29}+\dfrac{1}{29}-\dfrac{1}{39}+...+\dfrac{1}{2019}-\dfrac{1}{2029}\right)\)
\(N=\dfrac{9}{10}.\left(\dfrac{1}{9}-\dfrac{1}{2029}\right)\)
\(N=\dfrac{9}{10}.\dfrac{2020}{18261}\)
\(N=\dfrac{202}{2029}\)

Số hữu tỉ là tập hơn các số có thể viết được dưới dạng phân số (thương) a/b, trong đó a và b là các số nguyên nhưng b phải khác 0
Số hữu tỉ bao gồm số thập phân hữu hạn, số thập phân vô hạn tuần hoàn, tập hợp số nguyên.
Tập hợp các số hữu tỉ không hoàn toàn đồng nhất với tập hợp các phân số a/b, vì mỗi số hữu tỉ có thể biểu diễn bằng nhiều phân số khác nhau. Ví dụ như là 1/3,2/6,3/9 ... cùng biểu diễn một số hữu tỉ.
Tập hợp số hữu tỉ kí hiệu là Q
Tập hợp số hữu tỉ là tập hợp đếm được.
Tính chất của số hữu tỉ là:
- Nhân số hữu tỉ có dạng a/b * c/d = a.c/ b.d
- Chia số hữu tỉ có dạng a/ b : c/d = a.d/ b.c
Ví dụ:
Nhân số hữu tỉ: 2/3 * 4/5 = 2.4/ 3.5 = 8/15
Chia số hữu tỉ: 2/3 : 4/5 = 2.5/ 4.3= 10/ 12
Chúc bạn học tốt!


Em nhân hệ số với hệ số, biến nhân biến (cùng chữ á)
(xo)2 thì đưa về bằng 12
Em tự làm thử nhé, anh sẽ sửa!

\(a,\left\{{}\begin{matrix}AB=AC\left(\Delta ABC.cân.tại.A\right)\\\widehat{ABC}=\widehat{ACB}\left(\Delta ABC.cân.tại.A\right)\\AD.chung\end{matrix}\right.\Rightarrow\Delta ADB=\Delta ADC\left(ch-gn\right)\)
\(b,\)Áp dụng định lí Py-ta-go cho tam giác ABD vuông tại D
\(AD^2=AB^2-BD^2=36\\ \Rightarrow AD=6\left(cm\right)\)
\(c,\) Vì tam giác BAC cân tại A nên đường cao AD cũng là trung tuyến
Mà G là trọng tâm nên \(AG=\dfrac{2}{3}AD=\dfrac{2}{3}\cdot6=4\left(cm\right)\)


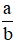 với a, b là các số nguyên; b ≠ 0.
với a, b là các số nguyên; b ≠ 0.




a) \(\left(-189\right)+135+\left(-111\right)+\left(-135\right)\)
\(=\left(-189-111\right)+\left(135-135\right)\)
\(=-300+0\)
\(=-300\)
b) \(126+345-126+215\)
\(=\left(126-126\right)+\left(345+215\right)\)
\(=0+560\)
\(=560\)
c) \(\left(-213\right)+186+\left|-213\right|-186+100\)
\(=\left(-213\right)+186+213-186+100\)
\(=\left(-213+213\right)+\left(186-186\right)+100\)
\(=0+0+100\)
\(=100\)
d) \(\left(-34\right)+\left|-123\right|+\left|-34\right|-123+200\)
\(=\left(-34\right)+123+34-123+200\)
\(=\left(-34+34\right)+\left(123-123\right)+200\)
\(=0+0+200\)
\(=200\)
e) \(\left(-250\right)+\left(-15\right)-\left(-250\right)+\left|-15\right|+150\)
\(=\left(-250\right)+\left(-15\right)+250+15+150\)
\(=\left(-250+250\right)+\left(-15+15\right)+150\)
\(=0+0+150\)
\(=150\)