Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a
xét tam giác MND & tam giác END
có ND chug
góc M=gócE(=90dộ)
góc MND=gócDNE
=> tam giác MND = tam giác END (g.c.g)
=> NE=NM(2 cạnh tươg ứg)
b
Từ cm câu a ta có NE=NM(2 cạnh tươg ứg) =>NE&NM cách đều ME => ND là đường trung trực của ME(t/c đg trug trực)
c
dựa vào địh lí pytago đảo
=> ND + NE = DE
=>10^2+NE^2=36^2
=>NE^2=36^2-10^2=(TỰ TÍNH MIK TÍNH KO RA)

hình bn tự kẻ nha ^^
a, vì N là phân giác \(\widehat{MNP}\)\(\left(gt\right)\Rightarrow\)\(\widehat{END}\)\(=\)\(\widehat{MND}\)
Xét tam giác MND và tam giác END có;
\(\widehat{M}\)\(=\)\(\widehat{E}\)\(=\)\(90\)độ ( gt)
CẠNH ND CHUNG
\(\widehat{MND}\)\(=\)\(\widehat{END}\)( CMT)
\(\Rightarrow\)TAM GIÁC MND \(=\)TAM GIÁC END (G-C-G)
a) Xét tam giác MND vuông tại M và tam giác END vuông tại E có :
ND : cạnh chung
MND=END ( ND phân giác MNE)
Vậy tam giác MND = tam giác END ( ch-gn)
b) Vì tam giác MND = tam giác END (cmt)
=>MN=EN(cctứ); MD=ED(cctứ)
Vì MN=EN(cmt)=> N thuộc đường trung trực của ME (1)
Vì MD=ED(cmt)=> D thuộc đường trung trực của ME(2)
Từ (1) và (2) => ND là đường trung trực của ME
c) Xét tam giác END vuông tại E có :
ED^2 + EN^2 = ND^2 (định lí Pytago)
NE^2 = ND^2 - ED^2
NE^2 = 10^2 - 6^2 = 100 - 36 = 64
=> NE = 8 (cm)
*ko hiểu sao rảnh mà lớp 8 đi giải bài lớp 7 :))))) *

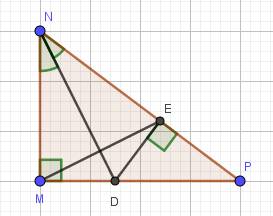
a) Xét hai tam giác vuông: \(\Delta MND\) và \(\Delta END\) có:
ND chung
\(\widehat{MND}=\widehat{END}\) (ND là phân giác của \(\widehat{MNP}\))
\(\Rightarrow\Delta MND=\Delta END\) (cạnh huyền-góc nhọn)
b) Do \(\Delta MND=\Delta END\left(cmt\right)\)
\(\Rightarrow MD=ED\) (hai cạnh tương ứng)
\(\Delta MED\) có MD = ED (cmt)
\(\Rightarrow\Delta MED\) cân tại D
c) Ta có:
\(\widehat{NDP}\) là góc ngoài của \(\Delta MND\)
\(\Rightarrow\widehat{NDP}=\widehat{NMD}+\widehat{MND}\)
\(=90^0+\widehat{MND}\)
\(\Rightarrow\widehat{NDP}\) là góc tù
\(\Delta NDP\) có \(\widehat{NDP}\) là góc tù
Mà góc tù là góc lớn nhất trong tam giác
\(\Rightarrow NP\) là cạnh lớn nhất (quan hệ giữa góc và cạnh đối diện trong \(\Delta NDP\))
\(\Rightarrow ND< NP\)

Xét ΔNMD vuông tại M và ΔNED vuông tại Ecó
ND chung
góc MND=góc END
=>ΔNMD=ΔNED

a: Xét ΔMNE vuông tại E và ΔKNE vuông tại E có
NE chung
góc MNE=góc KNE
=>ΔMNE=ΔKNE
b: Xét ΔNMD và ΔNKD có
NM=NK
góc MND=góc KND
ND chung
=>ΔNMD=ΔNKD
=>góc NKD=90 độ
=>DK vuông góc NP

a) xét tam giác MND và tam giác END ta có
MN = EN
góc MND = góc END
ND: cạnh chung
suy ra tam giác MND = tam giác END
suy ra DM = DE và óc NMD = góc NEDsuy ra góc NED = 90 độ
b) ta có tam giác MND = tam giác END suy ra MD = ED
xét tam giác DMK và tam giác DEP ta có
góc KMD = góc PED ( =90độ)
MD = ED
góc MDK = góc EDP( hai góc đối đinh)
suy ra tam giác DMK = tam giác DEP(đpcm)
c)ta có tam giác DMK = tam giác DEP suy ra MK=EP
ta có NM = NEvà MK = EP suy ra MN+MK=NE+EP suy ra NK=NP
xet tam giác KNDvà tam giác PND ta có
NK=NP
KND= PND
ND:cạnh chung
suy ra tam giác KND=tam giác PND suy ra góc NDK = góc NDP
ta có góc NDK+góc NDP=180 độ và góc NDK= góc NDP
suy góc NDK = góc NDP =90độ
suy ra ND vuông góc với KP

a: Xét ΔNMK co
NE vừa là đường cao, vừa là phân giác
=>ΔNMK cân tại N
=>NM=NK
Xét ΔNMD và ΔNKD có
NM=NK
góc MND=góc KND
ND chung
=>ΔMND=ΔKND
=>góc NKD=90 độ
=>DK vuông góc NP
b: Xét ΔNKM có
MH,NE là đường cao
MH cắt NE tại I
=>I là trực tâm
=>KI vuông góc MN
=>KI//MP