K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
8 tháng 3 2022
Câu 4:
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
Suy ra: BA=BH và EA=EH
b: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: AK=HC
Ta có: BA+AK=BK
BH+HC=BC
mà BA=BH
và AK=HC
nên BK=BC
hay ΔBKC cân tại B
c: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
NC
4
23 tháng 9 2021
Bài 1:
Ta có: \(A=\dfrac{x}{yz}:\dfrac{y}{zx}=\dfrac{x}{yz}.\dfrac{zx}{y}=\dfrac{x^2}{y^2}=\left(\dfrac{x}{y}\right)^2\)
Mà \(3x=2y\Leftrightarrow\dfrac{x}{y}=\dfrac{2}{3}\Leftrightarrow\left(\dfrac{x}{y}\right)^2=\dfrac{4}{9}\)
\(\Rightarrow A=\dfrac{4}{9}\)
23 tháng 9 2021
\(1,\\ 3x=2y\Rightarrow\dfrac{x}{y}=\dfrac{2}{3}\Rightarrow\dfrac{x}{yz}=\dfrac{2}{3z}\\ 3x=2y\Rightarrow\dfrac{y}{x}=\dfrac{3}{2}\Rightarrow\dfrac{y}{zx}=\dfrac{3}{2z}\)
\(2,\\ \dfrac{x}{y^2}=2\Rightarrow x=2y^2\\ \dfrac{x}{y}=16\Rightarrow x=16y\\ \Rightarrow2y^2=16y\Rightarrow2y\left(y-8\right)=0\\ \Rightarrow\left[{}\begin{matrix}y=0\left(ktm.vì.y\ne0\right)\\y=8\end{matrix}\right.\Rightarrow y=8\Rightarrow x=128\)
\(3,\\ \dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
6 tháng 10 2021
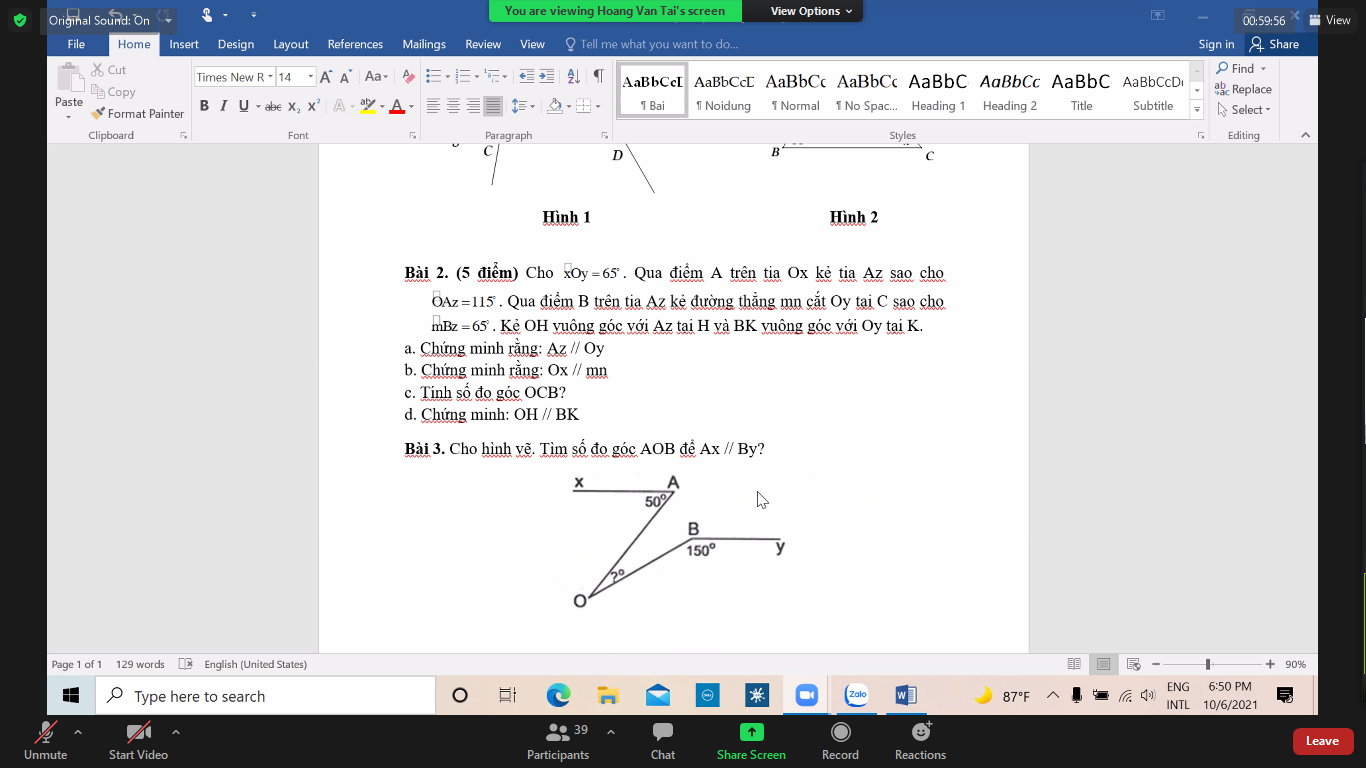
Giả sử Ax//By
Kẻ Ax//By//Oz
\(\Rightarrow\widehat{OAx}=\widehat{AOz}=50^0\)(so le trong)
Ta có: By//Oz
\(\Rightarrow\widehat{OBy}+\widehat{BOz}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{OBz}=180^0-150^0=30^0\)
Ta có: \(\widehat{AOB}=\widehat{AOz}-\widehat{BOz}=50^0-30^0=20^0\)
\(\Rightarrow x=20^0\)
VH
1
LM
Lê Minh Vũ
VIP
14 tháng 6 2023
\(2.16\ge2^n>4\)
\(2.2^4\ge2^n>2^2\)
\(2^5\ge2^n>2^2\)
=> \(n\in\left\{3,4,5\right\}\)
Vậy: \(n\in\left\{3,4,5\right\}\)
HL
1
RQ
3
AH
Akai Haruma
Giáo viên
24 tháng 12 2018
Lời giải:
Vì \(3x=5y\Rightarrow y=\frac{3}{5}x=0,6x\). Thay vào điều kiện thứ 2 ta có:
\(2x+3y=-39\)
\(\Leftrightarrow 2x+3.0,6x=-39\)
\(\Leftrightarrow 3,8x=-39\Rightarrow x=\frac{-195}{19}\)
\(\Rightarrow y=0,6x=0,6.\frac{-195}{19}=\frac{-117}{19}\)
Vậy \((x,y)=(\frac{-195}{19}; \frac{-117}{19})\)
S
24 tháng 12 2018
Ta có: \(3x=5y\Leftrightarrow\dfrac{x}{5}=\dfrac{y}{3}\Leftrightarrow\dfrac{2x}{10}=\dfrac{3y}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{2x}{10}=\dfrac{3y}{9}=\dfrac{2x+3y}{10+9}=\dfrac{-39}{19}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{-39}{19}\\\dfrac{y}{3}=\dfrac{-39}{19}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-195}{19}\\y=\dfrac{-177}{19}\end{matrix}\right.\)
Vậy, ...
Câu 1: A
Câu 2: D
Câu 3: A
Câu 4: A