
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Áp dụng tính chất của dãy tỉ số bằng nhau, ta được
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{b-a}{4-3}=23\)
Do đó: a=69; b=92

Ta có:4(2x+3y)+(9x+5y)=17(x+y)
Vì 2x+3y⋮17⇒4(2x+3y)⋮17
Mà tổng chia hết cho 17
⇒9x+5y⋮17
Ta có:1+2+3+4+...+9=(1+9).4+5=45
Vì mỗi lần xóa đi hai số bất kì x,y rồi thay bằng hiệu của chúng (x-y hoặc y-x tùy vào x>y hay x<y) thì tổng trên sẽ giảm đi x+y và tăng thêm x-y hoặc y-x
=> Tổng trên sẽ giảm đi x+y-(x-y)=2y hoặc x+y-(y-x)=2x
Ta lại có:2y và 2x là hai số chẵn mà tổng lẻ
=> Tổng ban đầu trừ đi số chẵn không thể bằng 0
Vậy ko có cách nào để kết quả bằng 0


\(3^{x+1}+3^{x+3}=810\)
\(\Leftrightarrow3^{x+1}+3^{x+1}.3^2=810\)
\(\Leftrightarrow3^{x+1}.10=810\)
\(\Leftrightarrow3^{x+1}=81=3^4\)
\(\Leftrightarrow x+1=4\)
\(\Leftrightarrow x=3\)

\(\left|3x-5\right|+\left(2y+5\right)^{208}+\left(4z-3\right)^{20}\le0\)
\(\Leftrightarrow\hept{\begin{cases}3x-5=0\\2y+5=0\\4z-3=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{5}{3}\\y=-\frac{5}{2}\\z=\frac{3}{4}\end{cases}}\)



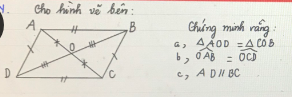


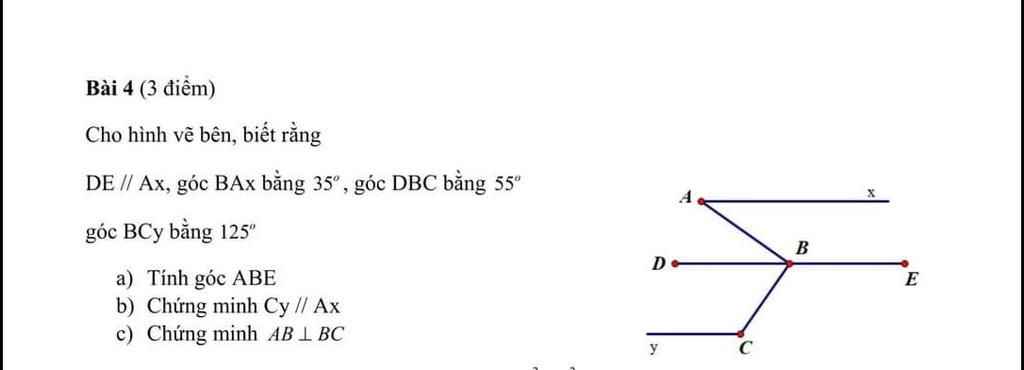
 mn giúp mk vs, mk cần gấp!!!cảm ơn trước ạ
mn giúp mk vs, mk cần gấp!!!cảm ơn trước ạ

a, Vì a//b mà a⊥AB nên b⊥AB
b, Vì a//b nên \(\widehat{CDB}+\widehat{ACD}=180^0\) (trong cùng phía)
Do đó \(\widehat{CDB}=180^0-120^0=60^0\)
c, Vì Ct là p/g nên \(\widehat{ICD}=\dfrac{1}{2}\widehat{ACD}=60^0\)
Xét tg CID có \(\widehat{CID}=180^0-\widehat{ICD}-\widehat{CDB}=180^0-60^0-60^0=60^0\)
d, Vì Dt' là p/g nên \(\widehat{BDt'}=\dfrac{1}{2}\widehat{BDy}=\dfrac{1}{2}\widehat{ACD}\left(đồng.vị\right)=60^0=\widehat{CID}\)
Mà 2 góc này ở vị trí so le trong nên Ct//Dt'