
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
200920 = 200910.200910 < 200910.1000110 = 2009200910
=> 200920 < 2009200910

a. ta có: AB = AE ( gt ) => tam giác ABE cân tại A
b.xét tam giác BAD và tam giác EAD có:
AB = AE ( gt )
góc BAD = góc EAD ( gt )
AD: cạnh chung
Vậy tam giác BAD = tam giác EAD ( c.g.c )
=> BD = ED ( 2 cạnh tương ứng )
a: Xét ΔABE có AB=AE
nên ΔABE cân tại A
b: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE
c: Ta có: ΔABD=ΔAED
nên \(\widehat{ABD}=\widehat{AED}=90^0\)
hay ED\(\perp\)AC
Ta có: BD=DE
mà DE<DC
nên BD<DC
d: Xét ΔADC có \(\widehat{DAC}=\widehat{C}\)
nên ΔADC cân tại D
=>DA=DC


-Giúp nhiều bài thế bạn, chẳng lẽ bạn không biết làm bài nào á?

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC

\(\Delta AHB=\Delta AHC\Rightarrow\widehat{AHB}=\widehat{AHC}\) (2 góc tương ứng)
Mà \(\widehat{AHB}+\widehat{AHC}=180^o\) (2 góc kề bù)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^o\)
\(\Rightarrow AH\perp BC\left(đpcm\right)\)
\(\Delta AHB=\Delta AHC\Rightarrow\widehat{AHB}=\widehat{AHC}\left(2.góc.tương.ứng\right)\)
Ta có:\(\widehat{AHB}+\widehat{AHC}=180^o\left(2.góc.kề.bù\right)\\ \Rightarrow2\widehat{AHB}=180^o\left(vì\widehat{AHB}=\widehat{AHC}\right)\\ \Rightarrow\widehat{AHB}=90^o\\ \Rightarrow AH\perp BC\)


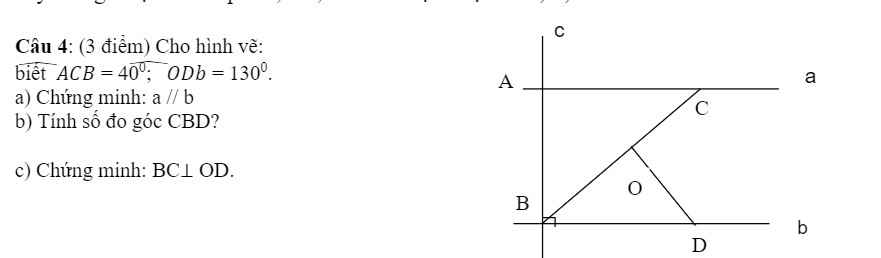 mk vs ạ
mk vs ạ


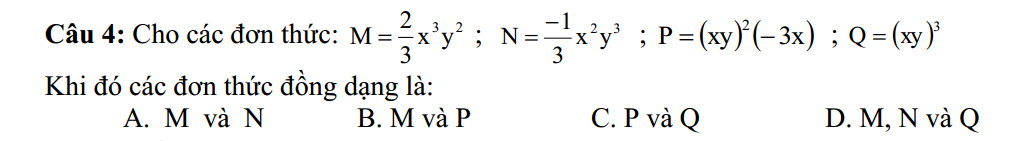 giúp mk vs, mk cần gấp
giúp mk vs, mk cần gấp

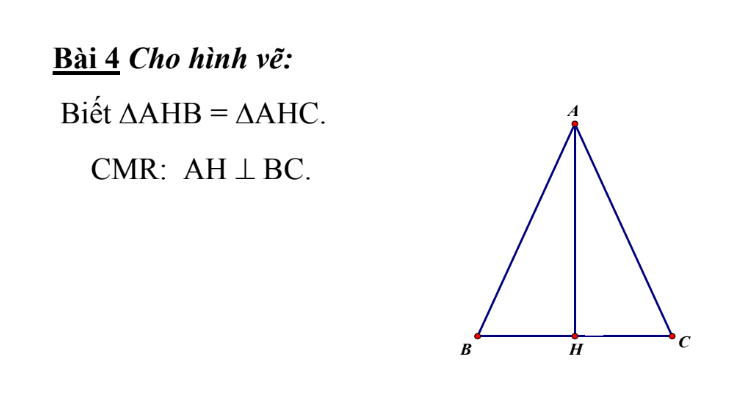 giúp mk vs, mk sẽ tick cho
giúp mk vs, mk sẽ tick cho giúp mk vs mk cảm ơn ạ
giúp mk vs mk cảm ơn ạ
a/b=c/d =>a/c=b/d
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)
\(\Rightarrow\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\left(\frac{a+b}{c+d}\right)^2\)\(\Leftrightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a+b}{c+d}\right)^2\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\left(\frac{a+b}{b+d}\right)^2=\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\)
\(\Rightarrow dpcm\)