
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 2
a, \(3\sqrt{8}\) + \(\sqrt{18}\) - \(\sqrt{72}\)
=\(6\sqrt{2}\)+\(3\sqrt{2}\)-\(6\sqrt{2}\)
=\(3\sqrt{2}\)(3+1-3)
=3\(\sqrt{2}\)

\(\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{4}{3}\)
\(\Leftrightarrow\dfrac{BD}{CD}=\dfrac{4}{3}\)
hay BD=100(cm)
Suy ra: HD=BD-BH=112-100=12(cm)
\(AD=\sqrt{AH^2+HD^2}=\sqrt{84^2+12^2}=60\sqrt{2}\left(cm\right)\)

b: Ta có: \(BD\cdot DA+CE\cdot EA\)
\(=HD^2+HE^2\)
\(=ED^2=AH^2\)

Câu 3:
2: Xét tứ giác OKEH có
\(\widehat{OKE}=\widehat{OHE}=\widehat{KOH}=90^0\)
Do đó: OKEH là hình chữ nhật
mà đường chéo OE là tia phân giác của \(\widehat{KOH}\)
nên OKEH là hình vuông



a) Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
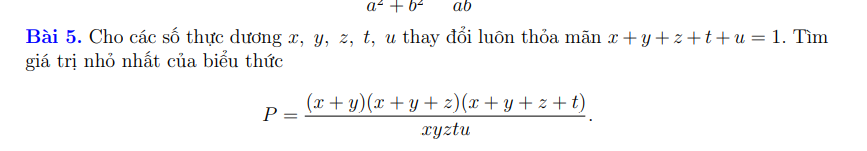






Hai bài này tương tự nhau, bạn có thể tham khảo nhé.
\(P\ge\dfrac{\left(x+y\right)\left(x+y+z\right)\left(x+y+z+t\right)}{\dfrac{1}{4}\left(x+y\right)^2ztu}=\dfrac{4\left(x+y+z\right)\left(x+y+z+t\right)}{\left(x+y\right)ztu}\)
\(P\ge\dfrac{4\left(x+y+z\right)\left(x+t\text{y}+z+t\right)}{\dfrac{1}{4}\left(x+y+z\right)^2tu}=\dfrac{16\left(x+y+z+t\right)}{\left(x+y+z\right)tu}\)
\(P\ge\dfrac{16\left(x+y+z+t\right)}{\dfrac{1}{4}\left(x+y+z+t\right)^2u}=\dfrac{64}{\left(x+y+z+t\right)u}\ge\dfrac{64}{\dfrac{1}{4}\left(x+y+z+t+u\right)^2}=256\)
Dấu "=" xảy ra khi \(\left(x;y;z;t;u\right)=\left(\dfrac{1}{16};\dfrac{1}{16};\dfrac{1}{8};\dfrac{1}{4};\dfrac{1}{2}\right)\)