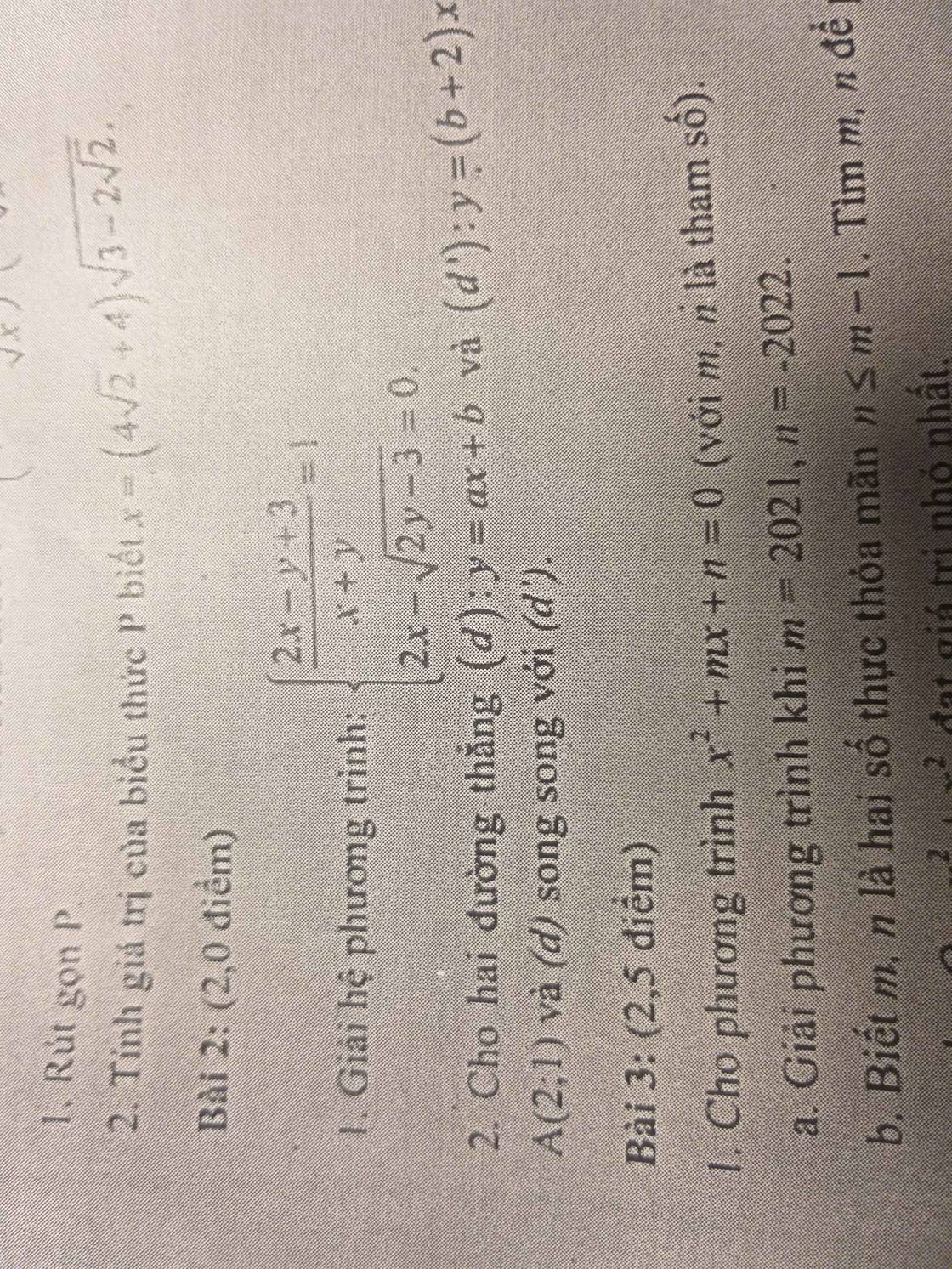K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
3 tháng 8 2021
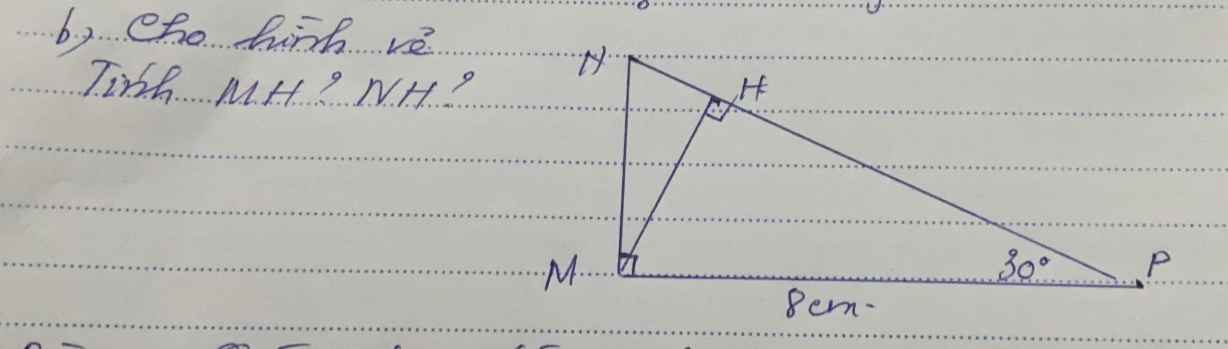
Áp dụng tỉ số lượng giác của góc nhọn vào \(\Delta MHP\), ta có:
\(\cos30\text{°}=\dfrac{MH}{8}\Rightarrow MH=8.\cos30\text{°}=4\sqrt{3}\left(cm\right)\)
Mặt khác, \(\text{∠}MNP=90\text{°}-30\text{°}=60\text{°}\)
Áp dụng tí số lượng giác của góc nhọn vào \(\Delta MHN\), ta có:
\(\tan60\text{°}=\dfrac{4\sqrt{3}}{NH}\Rightarrow NH=4\sqrt{3}.\tan60\text{°}=12\left(cm\right)\)
AH
Akai Haruma
Giáo viên
3 tháng 8 2021
Lời giải:
Xét tam giác $MHP$ vuông tại $H$ thì:
$\frac{MH}{MP}=\sin P=\sin 30^0=\frac{1}{2}$
$\Rightarrow MH=\frac{MP}{2}=4$ (cm)
Theo định lý Pitago:
$HP=\sqrt{MP^2-MH^2}=\sqrt{8^2-4^2}=4\sqrt{3}$
Theo hệ thức lượng trong tam giác vuông:
$MH^2=NH.HP$
$\Leftrightarrow 4^2=4\sqrt{3}.NH$
$\Leftrightarrow NH=\frac{4\sqrt{3}}{3}$ (cm)
21 tháng 12 2021
a: Xét hình thang ADCB có
O là trung điểm của AB
OM//AD//CB
Do đó: M là trung điểm của CD
hay MC=MD
23 tháng 6 2023
14:
a: Để hai đường cắt nhau trên trục tung thì m-1=15-3m
=>4m=16
=>m=4
b: Khi m=4 thì (d1): y=-4x+3 và (d2): y=4/3x+3
Tọa độ A là:
y=0 và -4x+3=0
=>x=3/4 và y=0
Tọa độ B là:
y=0 và 4/3x+3=0
=>x=-3:4/3=-9/4 và y=0
c: C(0;3); A(3/4;0); B(-9/4;0)
AB=căn (-9/4-3/4)^2+(0-0)^2=3
AC=căn (3/4-0)^2+3^2=3/4*căn 17
BC=căn (-9/4-0)^2+(3-0)^2=15/4
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{\sqrt{17}}{17}\)
=>sinA=4/căn 17
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=\dfrac{9}{2}\)
\(C=3+\dfrac{3}{4}\sqrt{17}+\dfrac{15}{4}=\dfrac{27}{4}+\dfrac{3}{4}\sqrt{17}\)
d: AB=3; AC=3/4*căn 17; BC=15/4
sin A=4/căn 17
=>AB/sinC=AC/sinB=BC/sinA
=>góc A=76 độ; 3/sinC=3/4*căn 17/sinB=15*căn 17/16
=>sin C=16*căn 17/85; sin B=4/5
=>góc B=53 độ; góc C=51 độ
29 tháng 8 2021
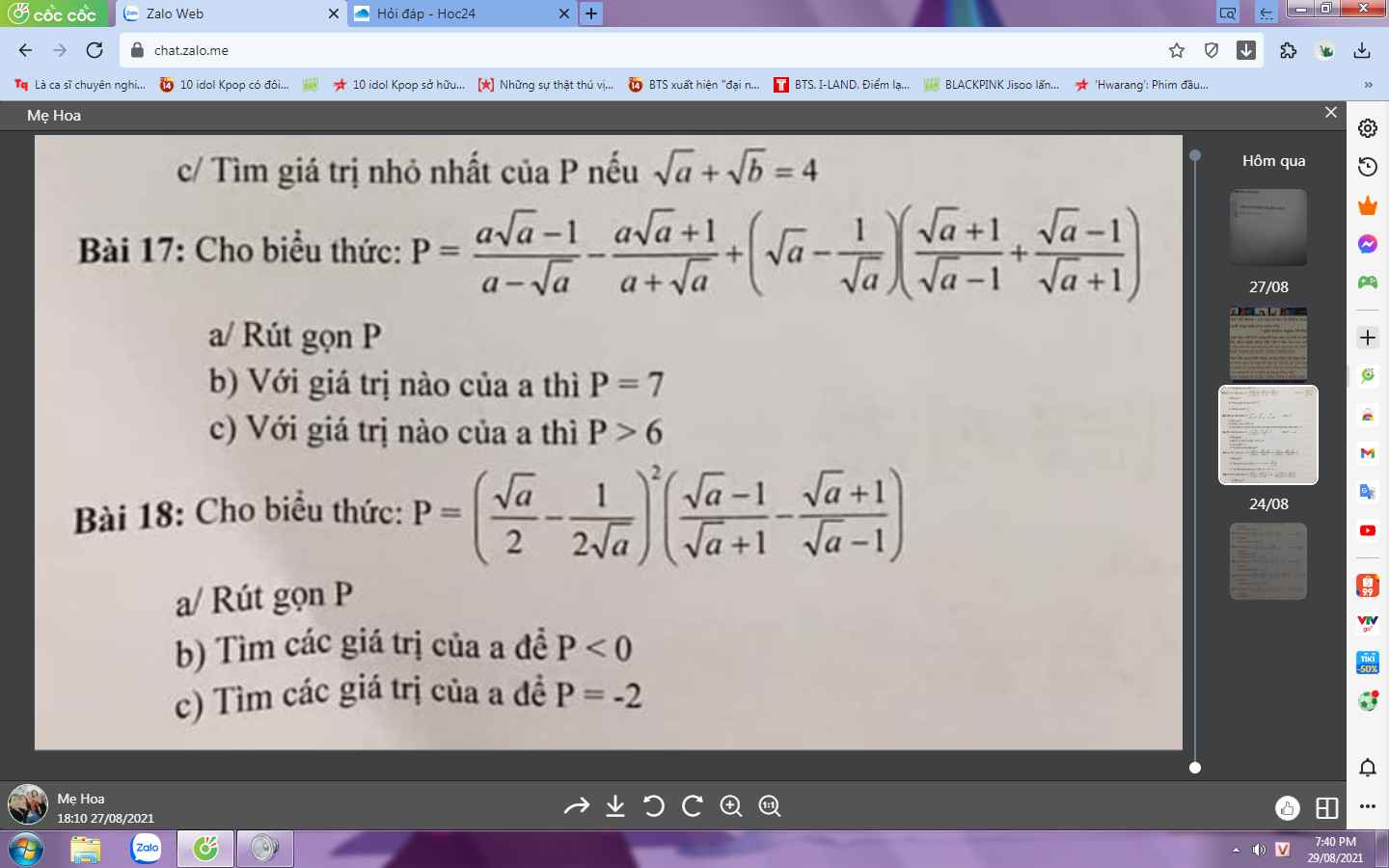
Bài 18:
a: Ta có: \(P=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2\cdot\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)^2\cdot\left(\sqrt{a}+1\right)^2}{4a}\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{\left(a-1\right)\cdot\left(-4\right)\cdot\sqrt{a}}{4a}\)
\(=\dfrac{-a+1}{\sqrt{a}}\)
b: Để P<0 thì -a+1<0
\(\Leftrightarrow-a< -1\)
hay a>1
c: Để P=-2 thì \(-a+1=-2\sqrt{a}\)
\(\Leftrightarrow-a+1+2\sqrt{a}=0\)
\(\Leftrightarrow a-2\sqrt{a}+1=2\)
\(\Leftrightarrow\left(\sqrt{a}-1\right)^2=2\)
\(\Leftrightarrow\sqrt{a}-1=\sqrt{2}\)
hay \(a=3+2\sqrt{2}\)
29 tháng 8 2021
Bài 17:
a: Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}-1}{\sqrt{a}+1}\right)\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{a-1}\)
\(=2+\dfrac{2a+2}{\sqrt{a}}\)
\(=\dfrac{2a+2\sqrt{a}+2}{\sqrt{a}}\)
XM
3 tháng 5 2023
ĐK: \(\left\{{}\begin{matrix}x\ne-y\\y\ge\dfrac{3}{2}\end{matrix}\right.\).
\(\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}=1\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-1=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-\dfrac{x+y}{x+y}=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y+3-x-y=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y+3=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-\left(2y-3\right)=0\\2x-\sqrt{2y-3}=0\end{matrix}\right..\)
Đặt a = x, b = \(\sqrt{2y-3}\).
Hệ phương trình trở thành: \(\left\{{}\begin{matrix}a-b^2=0\\2a-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\2b^2-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\b\left(2b-1\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}a=0\\a=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y-3=\dfrac{1}{4}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y=\dfrac{13}{4}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\y=\dfrac{13}{8}\end{matrix}\right.\end{matrix}\right..\)
Vậy hệ phương trình có nghiệm (x;y) \(\in\) \(\left\{\left(0;\dfrac{3}{2}\right),\left(\dfrac{1}{4};\dfrac{13}{8}\right)\right\}\).
27 tháng 8 2021
Xét tứ giác BCDE có
\(\widehat{D}+\widehat{CBE}=180^0\)
nên BCDE là tứ giác nội tiếp
Suy ra: B,C,D,E cùng thuộc 1 đường tròn
Tâm là trung điểm của CE
10 tháng 9 2021
a:Gọi OK là khoảng cách từ O đến MN
Suy ra: K là trung điểm của MN
Xét ΔOKM vuông tại K, ta được:
\(OM^2=KM^2+OK^2\)
hay OK=6(cm)
