K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
27 tháng 8 2021
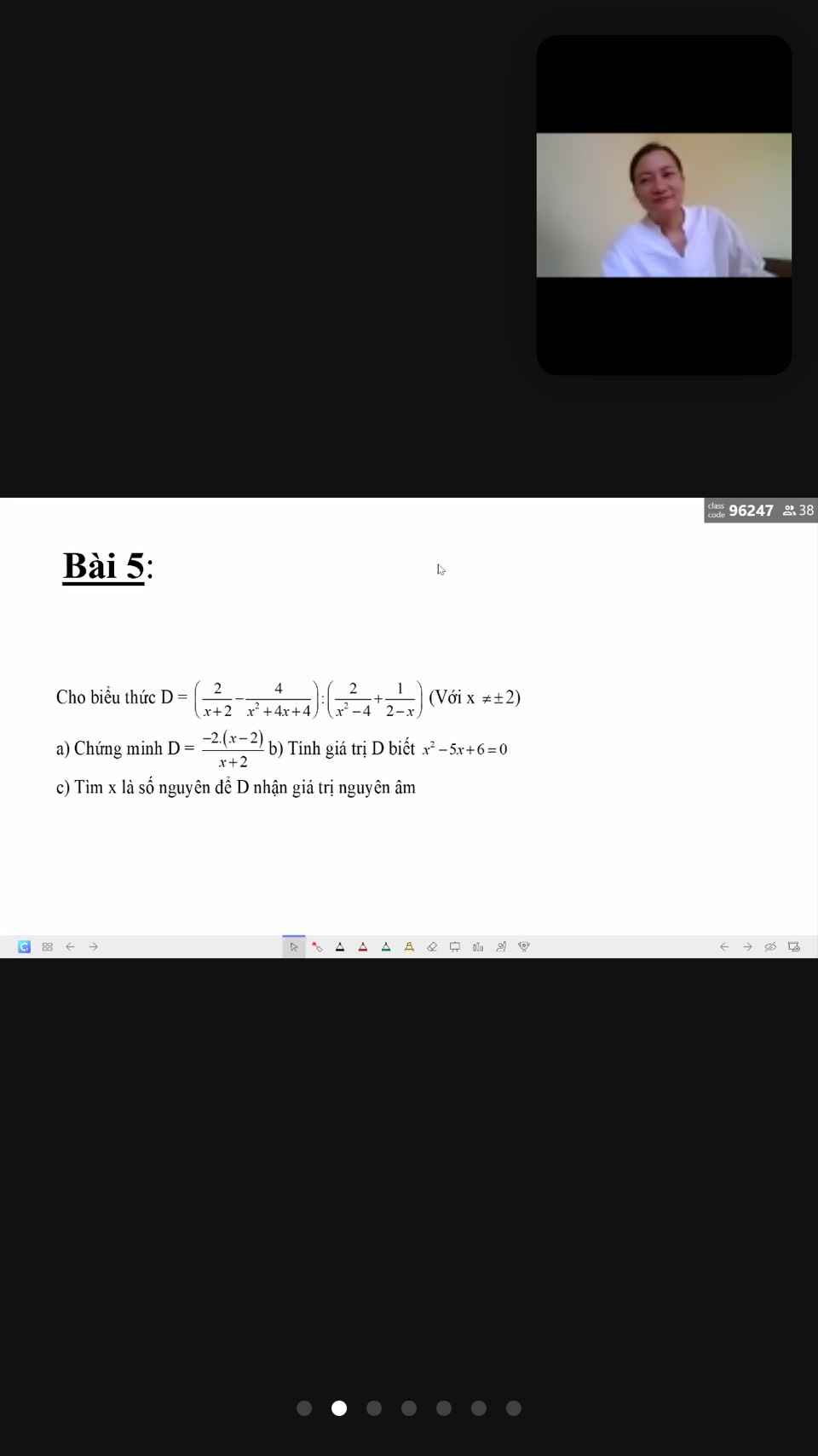
a) \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)\(=\left(\dfrac{2}{x+2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}\right)\)
\(=\left(\dfrac{2\left(x+2\right)}{\left(x+2\right)^2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\right)\)
\(=\dfrac{2\left(x+2\right)-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{-x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}.\dfrac{\left(x-2\right)\left(x+2\right)}{-x}\)
\(=\dfrac{-2.\left(x-2\right)}{x+2}\)
\(x^2-5x+6=0\\ \Rightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Rightarrow\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(P=\dfrac{-2.\left(x-2\right)}{x+2}\)
Thay \(x=2\), ta có:
\(P=\dfrac{-2.\left(2-2\right)}{2+2}\)
\(=0\)
Thay \(x=3\), ta có:
\(P=\dfrac{-2.\left(3-2\right)}{3+2}\)
\(=-\dfrac{2}{5}\)
BB
1
6 tháng 1 2023
Bài 5:
a: 2x-(3-5x)=4(x+3)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>x=5
b: =>5/3x-2/3+x=1+5/2-3/2x
=>25/6x=25/6
=>x=1
c: 3x-2=2x-3
=>3x-2x=-3+2
=>x=-1
d: =>2u+27=4u+27
=>u=0
e: =>5-x+6=12-8x
=>-x+11=12-8x
=>7x=1
=>x=1/7
f: =>-90+12x=-45+6x
=>12x-90=6x-45
=>6x-45=0
=>x=9/2
31 tháng 10 2021
1)\(6x-x^2=x\left(6-x\right)\)
2)\(5x^2z-15xyz+30xz^2=5x\left(xz-3y+6z\right)\)
3)\(x^3-6x^2+9x=x\left(x^2-6x+9\right)=x\left(x-3\right)^2\)
NK
1
12 tháng 9 2021
f: \(3ab-6a+b-2\)
\(=3a\left(b-2\right)+\left(b-2\right)\)
\(=\left(b-2\right)\left(3a+1\right)\)
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
a.
\(G=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{(2x-3)(x+1)-(2x+1)(x-1)}{(x-1)(x+1)}\)
\(=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{-2}{(x-1)(x+1)}=\frac{x^2-4}{x+1}+\frac{2}{x+1}.\frac{(x+1)(x-1)}{-2}\)
\(=\frac{x^2-4}{x+1}-(x-1)=\frac{x^2-4-(x^2-1)}{x+1}=\frac{-3}{x+1}\)
b.
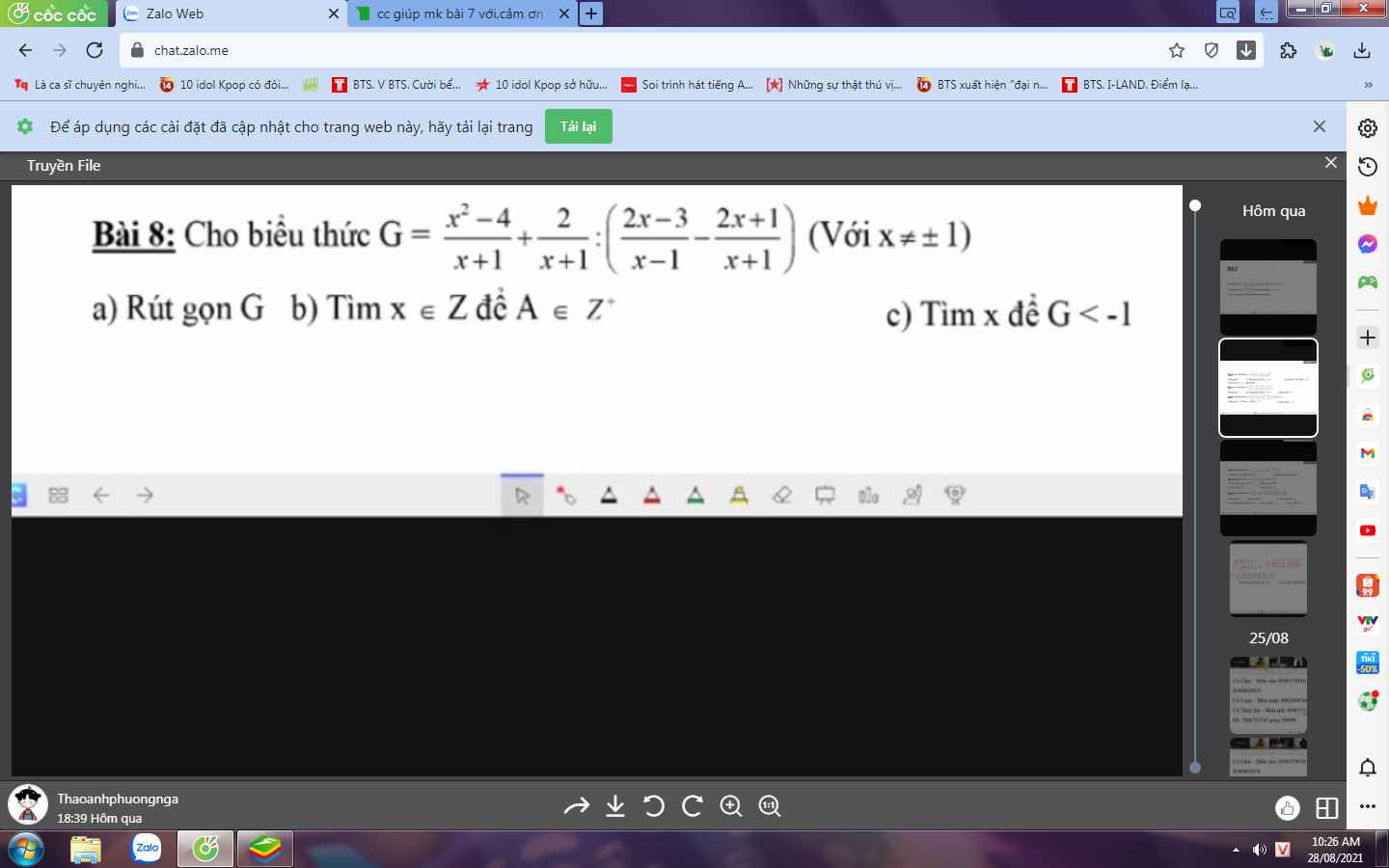
Để $A\in\mathbb{Z}^+$ thì $x+1$ là ước âm của $-3$
$\Rightarrow x+1\in\left\{-1;-3\right\}$
$\Leftrightarrow x\in\left\{-2;-4\right\}$ (tm)
c.
$G< -1\Leftrightarrow \frac{-3}{x+1}+1< 0$
$\Leftrightarrow \frac{x-2}{x+1}< 0$
$\Leftrightarrow x-2<0< x+1$ hoặc $x-2>0>x+1$
$\Leftrightarrow -1< x< 2$ (chọn) hoặc $-1> x>2$ (loại)
Vậy $-1< x< 2$ và $x\neq 1$
28 tháng 8 2021
Bài 8:
a: Ta có: \(G=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\left(\dfrac{2x-3}{x-1}-\dfrac{2x+1}{x+1}\right)\)
\(=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\dfrac{2x^2+2x-3x-3-2x^2+2x-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{2}{x+1}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{-2}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{-x+1}{1}\)
\(=\dfrac{x^2-4-\left(x-1\right)\left(x+1\right)}{x+1}\)
\(=\dfrac{x^2-4-x^2+1}{x+1}\)
\(=-\dfrac{3}{x+1}\)
17 tháng 3 2016
Xét tam giác ODC có:
AB/CD=1/2 (gt)
OA/OC=1/2 (OA/AC=1/3)
=>AB//CD(d/l Ta-lét)
=> ABCD là hình thang
=> bạn hãy cố gắng làm tiếp nếu có thể
hãy tìm các cặp diện tích tam giác bằng nhau, chứ mik ko chắc nữa
MA
2
15 tháng 11 2021
\(d,=\dfrac{3y}{5x\left(x-y\right)}\\ e,=\dfrac{5x\left(x+2\right)\left(2-x\right)}{4\left(x-2\right)\left(x+2\right)}=\dfrac{-5x}{4}\\ f,=\dfrac{3\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)\left(6-x\right)}=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\\ g,=\dfrac{3xy\left(x-3y\right)\left(x+3y\right)}{2x^2y^2\left(x-3y\right)}=\dfrac{3\left(x+3y\right)}{2xy}\\ h,=\dfrac{45x^2y\left(x-y\right)\left(x+y\right)}{10xy\left(y-x\right)}=\dfrac{-9x\left(x+y\right)}{2}\\ i,=\dfrac{12\left(a-b\right)\left(a+b\right)\left(a^2+ab+b^2\right)}{3\left(a+b\right)\left(a-b\right)^2}=\dfrac{4\left(a^2+ab+b^2\right)}{a-b}\)
15 tháng 11 2021
e: \(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-10}{4}=-\dfrac{5}{2}\)
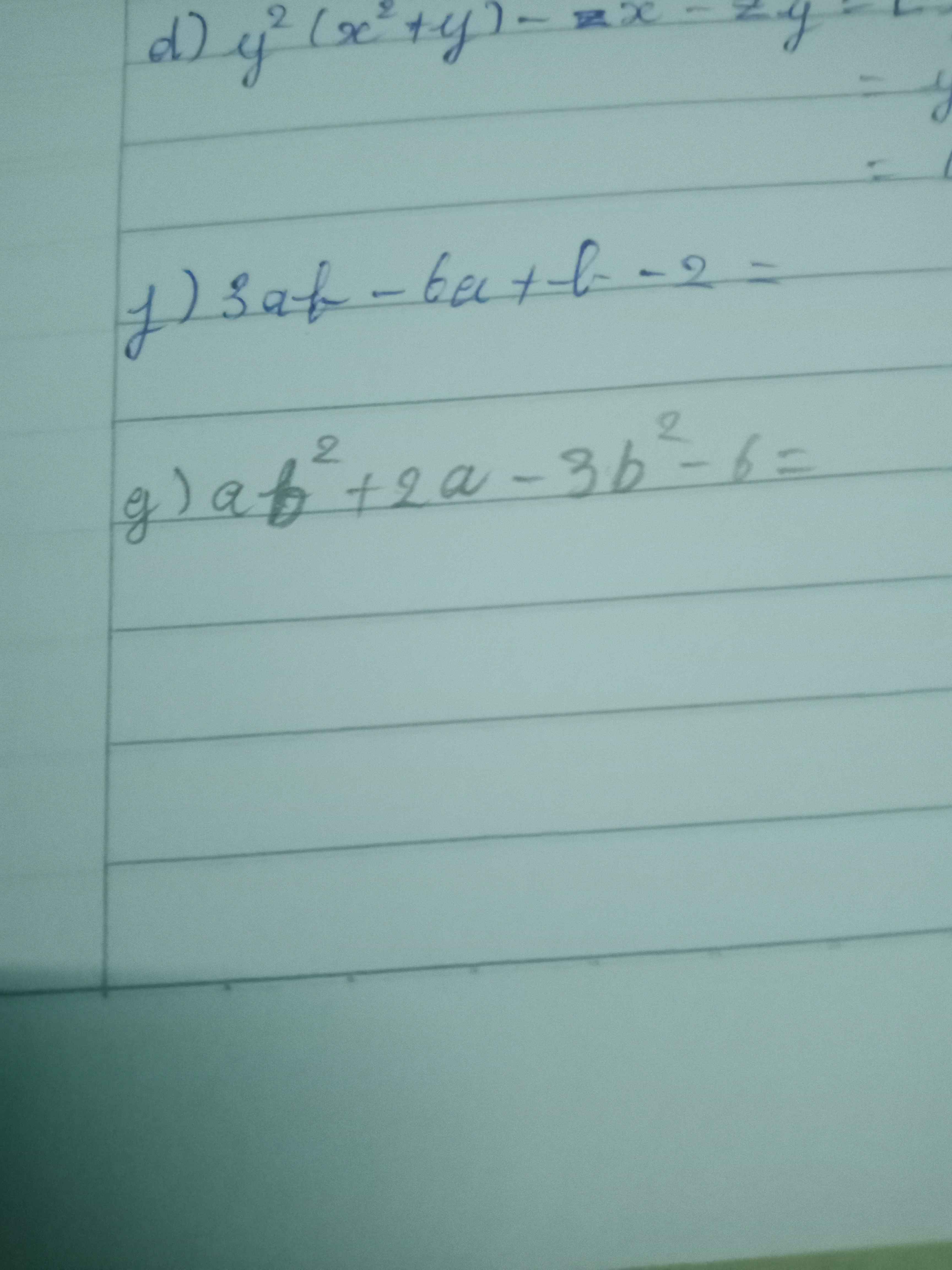
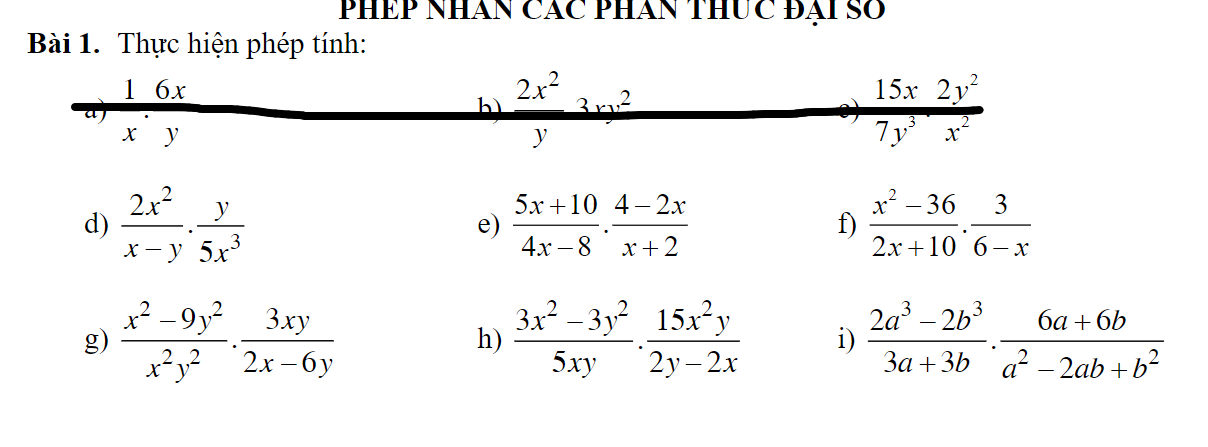
đã chụp khó nhìn r mà còn lại thi nữa , combo x2 :'((
Câu 6: B
Câu 7: D
Câu 8: B