K
Khách
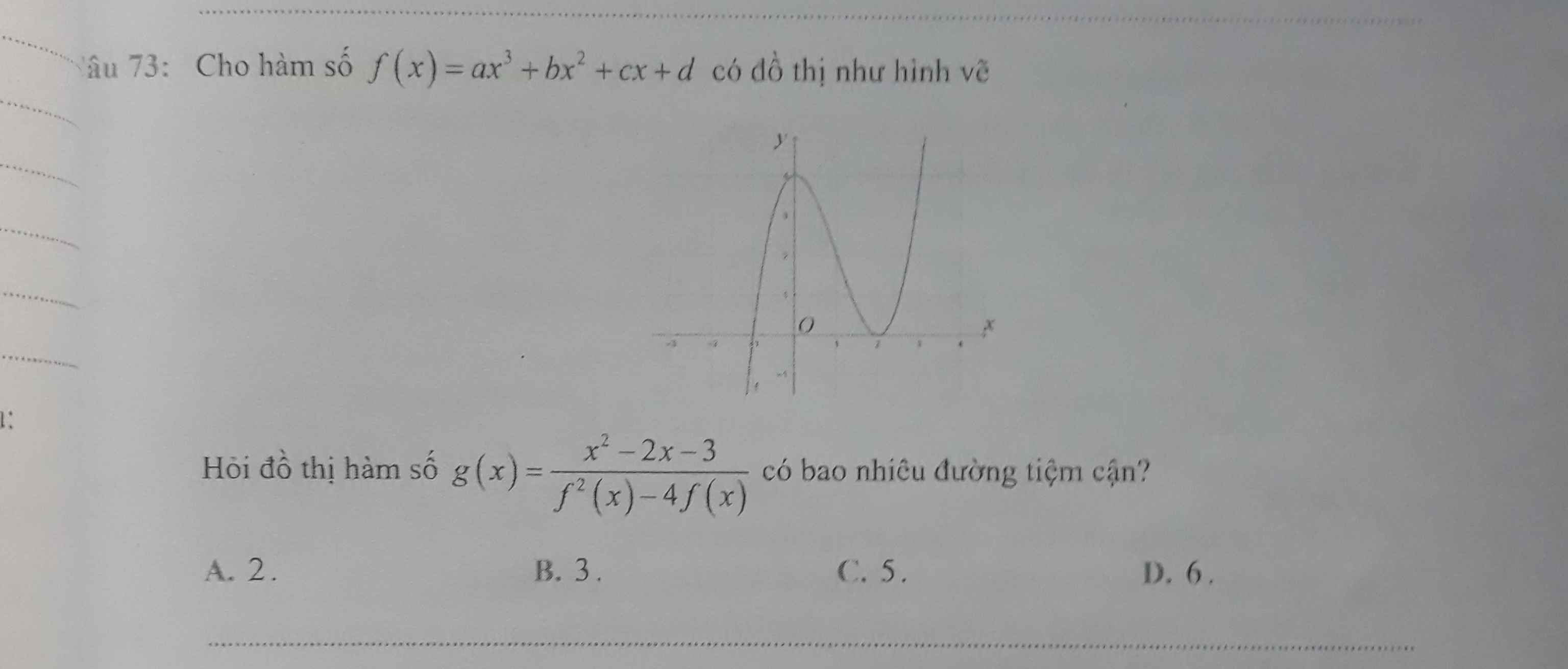
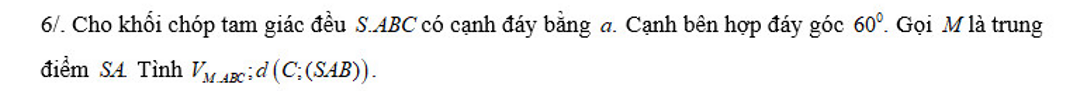Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2021
Gọi đường sinh là l, bán kính đáy R, chiều cao SO là h
Do thiết diện qua trục là tam giác vuông nên thiết diện là tam giác vuông cân
\(\Rightarrow SO=R\Rightarrow h=R\)
Áp dụng định lý cos: \(AB=\sqrt{OA^2+OB^2-2OA.OB.cos120^0}=R\sqrt{3}\)
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) ; \(AH=\dfrac{AB}{2}=\dfrac{R\sqrt{3}}{2}\)
\(OH=\sqrt{OA^2-AH^2}=\dfrac{R}{2}\)
Kẻ \(OK\perp SH\Rightarrow OK\perp\left(SAB\right)\Rightarrow OK=d\left(O;\left(P\right)\right)\)
\(\dfrac{1}{SO^2}+\dfrac{1}{OH^2}=\dfrac{1}{OK^2}\Rightarrow\dfrac{1}{R^2}+\dfrac{4}{R^2}=\dfrac{5}{3a^2}\Rightarrow R=a\sqrt{3}\)
\(V=\dfrac{1}{3}\pi R^2h=\dfrac{1}{3}\pi R^3=\pi a^3\sqrt{3}\)
d
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
Đặt \(log_2x=t\Rightarrow t\ge4\)
Phương trình trở thành: \(\sqrt{t^2-2t-3}=m\left(t-3\right)\)
\(\Leftrightarrow\sqrt{\left(t+1\right)\left(t-3\right)}=m\left(t-3\right)\)
\(\Leftrightarrow\sqrt{t+1}=m\sqrt{t-3}\)
\(\Leftrightarrow m=\sqrt{\dfrac{t+1}{t-3}}\)
Hàm \(f\left(t\right)=\sqrt{\dfrac{t+1}{t-3}}\) nghịch biến khi \(t\ge4\)
\(\lim\limits_{t\rightarrow+\infty}\sqrt{\dfrac{t+1}{t-3}}=1\) ; \(f\left(4\right)=\sqrt{5}\)
\(\Rightarrow1< f\left(t\right)\le\sqrt{5}\Rightarrow1< m\le\sqrt{5}\)
Đáp án D
MA
0
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2021
Đề bài bị sai
Gọi H là trung điểm AB thì \(SH\perp\left(ABCD\right)\Rightarrow\widehat{SCH}=60^0\)
\(\Rightarrow CH=\dfrac{SH}{tan60^0}=\dfrac{SH}{\sqrt{3}}\)
Mặt khác tam giác SAB đều \(\Rightarrow\widehat{SBH}=60^0\Rightarrow BH=\dfrac{SH}{tan60^0}=\dfrac{SH}{\sqrt{3}}\)
\(\Rightarrow CH=BH\) (vô lý do tam giác BCH vuông tại B theo giả thiết. Mà CH là cạnh huyền, BH là cạnh góc vuông, 2 cạnh này không thể bằng nhau)
VA
0
TH
1
KR
28 tháng 1 2023
\(I=\int\dfrac{2}{2+5sinxcosx}dx=\int\dfrac{2sec^2x}{2sec^2x+5tanx}dx\\ =\int\dfrac{2sec^2x}{2tan^2x+5tanx+2}dx\)
We substitute :
\(u=tanx,du=sec^2xdx\\ I=\int\dfrac{2}{2u^2+5u+2}du\\ =\int\dfrac{2}{2\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{8}}du\\ =\int\dfrac{1}{\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{16}}du\\ \)
Then,
\(t=u+\dfrac{5}{4}\\I=\int\dfrac{1}{t^2-\dfrac{9}{16}}dt\\ =\int\dfrac{\dfrac{2}{3}}{t-\dfrac{3}{4}}-\dfrac{\dfrac{2}{3}}{t+\dfrac{3}{4}}dt\)
Finally,
\(I=\dfrac{2}{3}ln\left(\left|\dfrac{t-\dfrac{3}{4}}{t+\dfrac{3}{4}}\right|\right)+C=\dfrac{2}{3}ln\left(\left|\dfrac{tanx+\dfrac{1}{2}}{tanx+2}\right|\right)+C\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
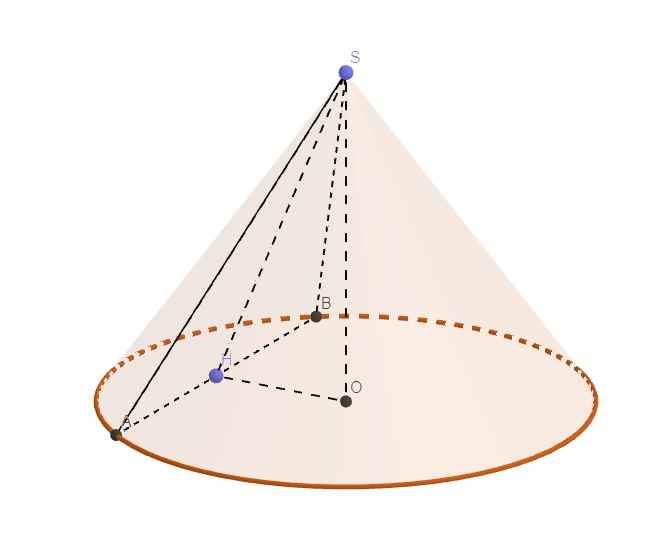
Đặt tên các điểm như hình vẽ, với H là trung điểm AB
\(\Rightarrow\widehat{SHO}=60^0\) (là góc giữa thiết diện và đáy nón)
Tam giác SAB đều \(\Rightarrow SH=\dfrac{AB\sqrt{3}}{2}=2\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow\left\{{}\begin{matrix}OH=SH.cos60^0=\sqrt{3}\\h=SO=SH.sin60^0=3\end{matrix}\right.\)
\(R=OA=\sqrt{AH^2+OH^2}=\sqrt{2^2+3}=\sqrt{7}\)
\(\Rightarrow V=\dfrac{1}{3}\pi R^2h=\dfrac{1}{3}\pi.7.3=7\pi\left(cm^3\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 5 2021
Phương trình mặt phẳng (P) qua A và vuông góc \(\overrightarrow{a}\) có dạng:
\(4\left(x-1\right)+2\left(y-1\right)-1\left(z+2\right)=0\)
\(\Leftrightarrow4x+2y-z-8=0\)
Gọi B là giao điểm (P) và \(\Delta\Rightarrow\) tọa độ B thỏa mãn:
\(4\left(2-t\right)+2\left(3+2t\right)-\left(1+3t\right)-8=0\) \(\Rightarrow t=\dfrac{5}{3}\) \(\Rightarrow B\left(\dfrac{1}{3};\dfrac{19}{3};6\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(-\dfrac{2}{3};\dfrac{16}{3};8\right)=\dfrac{2}{3}\left(-1;8;12\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=1-t\\y=1+8t\\z=-2+12t\end{matrix}\right.\)
