
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


nó bị lỗi nên mình làm câu khác rồi
câu hỏi đây nè bạn
Tìm GTLN của \(A=\dfrac{\left(x+2\right)^2}{2}\times\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+6x+4}{x}\)

Bài 1:
\(a,VT=\dfrac{3x-1}{\left(x+2\right)\left(3x-1\right)}=\dfrac{1}{x+2}=VP\\ b,VT=\dfrac{x^2+2x+4}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{1}{x-2}\\ VP=\dfrac{x+3}{\left(x+3\right)\left(x-2\right)}=\dfrac{1}{x-2}\\ \Rightarrow VT=VP\\ c,VT=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{2\left(x-2\right)}=\dfrac{x^2+2x+4}{2}=VP\)
Bài 2:
\(a,A=\dfrac{\left(x-4\right)\left(x+4\right)}{x-4}=x+4=2019+4=2023\\ b,2x-1=0\Leftrightarrow x=\dfrac{1}{2}\\ B=\dfrac{2x\left(x-1\right)}{\left(x-1\right)\left(x-2\right)}=\dfrac{2x}{x-2}=\dfrac{2\cdot\dfrac{1}{2}}{\dfrac{1}{2}-2}=\dfrac{1}{-\dfrac{3}{2}}=-\dfrac{2}{3}\\ c,x^2-9=0\Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=-3\left(tm\right)\end{matrix}\right.\Leftrightarrow x=-3\\ P=\dfrac{x-3}{\left(x-3\right)\left(x-2\right)}=\dfrac{1}{x-2}=\dfrac{1}{-3-2}=-\dfrac{1}{5}\)
Bài 3:
\(a,A=\dfrac{2\left(2x-3\right)}{2x^2-7x+6}=\dfrac{2\left(2x-3\right)}{\left(x-2\right)\left(2x-3\right)}=\dfrac{2}{x-2}\\ b,A=\dfrac{\left(x^2+2x\right)\left(2x^2-3x-2\right)}{x^2-2x}=\dfrac{x\left(x+2\right)\left(x-2\right)\left(2x+1\right)}{x\left(x-2\right)}=\left(x+2\right)\left(2x+1\right)\)


\(a,=\dfrac{x^2-4}{x+2}=\dfrac{\left(x-2\right)\left(x+2\right)}{x+2}=x-2\\ b,=\dfrac{x-5+2x+10-2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}=\dfrac{1}{x+5}\)


Xét ΔAMN vuông tại A có
\(MN^2=AM^2+AN^2\)
hay MN=20(cm)
Xét ΔABC có MN//BC
nên MN/BC=AM/AB=2/3
=>20/BC=2/3
hay y=30(cm)

a: Thay x=-4 vào B, ta được:
\(B=\dfrac{1-2\cdot\left(-4\right)}{2-\left(-4\right)}=\dfrac{1+8}{2+4}=\dfrac{9}{6}=\dfrac{3}{2}\)

 Giúp em vs.Em cần gấp.Cảm ơn trc ạ
Giúp em vs.Em cần gấp.Cảm ơn trc ạ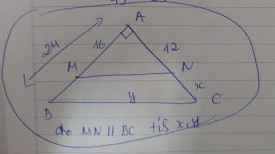
a,\(P\left(x\right)=x^3-2x^4+x^5-\dfrac{1}{2}x^2+=x^5-2x^4+x^3-\dfrac{1}{2}x^2+1\)
bậc :5
b,\(Q\left(x\right)=-x^3+3x^2-5x^4-x^2+3x^3-\dfrac{1}{2}=-5x^4+2x^3+2x^2-\dfrac{1}{2}\)
bậc :4
b,\(P\left(x\right)-Q\left(x\right)=\left(x^5-2x^4+x^3-\dfrac{1}{2}x^2+1\right)-\left(-5x^4+2x^3+2x^2-\dfrac{1}{2}\right)\)
\(=\text{}\text{}\text{}\text{}x^5+3x^4-x^3-\dfrac{5}{2}x^2+\dfrac{3}{2}\)