K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Y
29 tháng 6 2023
\(a.x^3+12x^2+48x+64=x^3+3.4x^2+3.4^2x+4^3=\left(x+4\right)^3\)
Thay \(x=6\) vào \(\left(x+4\right)^3=\left(6+4\right)^3=10^3=1000\)
\(b,B=x^3-6x^2+12x-8=\left(x-2\right)^3\)
Thay \(x=22\) vào \(\left(x-2\right)^3=\left(22-2\right)^3=20^3=8000\)
\(c,C=x^3+9x^2+27x+27=x^3+3.3x^2+3.3^2x+3^3=\left(x+3\right)^3\)
Thay \(x=-103\) vào \(\left(x+3\right)^3=\left(-103+3\right)^3=\left(-100\right)^3=-1000000\)
\(d,D=x^3-15x^2+75x-125=x^3-3.5x^2+5^2.3x-5^3=(x-5)^3\)
Thay \(x=25\) vào \(\left(x-5\right)^3=\left(25-5\right)^3=20^3=8000\)
H9
HT.Phong (9A5)
CTVHS
29 tháng 6 2023
a) \(A=x^3+12x^2+48x+64\)
\(=x^3+3\cdot4\cdot x^2+3\cdot4^2\cdot x+4^3\)
\(=\left(x+4\right)^3\)
Thay \(x=6\) vào biểu thức A ta có:
\(\left(6+4\right)^3=10^3=1000\)
Vậy: ...
b) \(B=x^3-6x^2+12x-8\)
\(=x^3-3\cdot2\cdot x^2+3\cdot2^2\cdot x-2^3\)
\(=\left(x-2\right)^3\)
Thay \(x=22\) vào biểu thức B ta có:
\(\left(22-2\right)^3=20^3=8000\)
Vậy: ...
c) \(C=x^3+9x^2+27x+27\)
\(=x^3+3\cdot3\cdot x^2+3\cdot3^2\cdot x+3^3\)
\(=\left(x+3\right)^3\)
Thay \(x=-103\) vào biểu thức C ta được:
\(\left(-103+3\right)^3=\left(-100\right)^3=-1000000\)
Vậy: ...
d) \(D=x^3-15x^2+75x-125\)
\(=x^3-3\cdot5\cdot x^2+3\cdot5^2\cdot x-5^3\)
\(=\left(x-5\right)^3\)
Thay \(x=25\) vào biểu thức D ta được:
\(\left(25-5\right)^3=20^3=8000\)
Vậy: ...
H9
HT.Phong (9A5)
CTVHS
30 tháng 6 2023
a) \(\left(x-3\right)\left(x^2+3x+9\right)-x\left(x+2\right)\left(2-x\right)=1\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(x-2\right)=1\)
\(\Leftrightarrow\left(x^3-3^3\right)-x\left(x+2\right)\left(x-2\right)=1\)
\(\Leftrightarrow x^3-27-x\left(x^2-2^2\right)=1\)
\(\Leftrightarrow x^3-27-x^3+4x=1\)
\(\Leftrightarrow4x-27=1\)
\(\Leftrightarrow4x=28\)
\(\Leftrightarrow x=7\)
b) \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow\left[\left(x+1\right)-\left(x-1\right)\right]\left[\left(x+1\right)^2+\left(x-1\right)\left(x+1\right)+\left(x-1\right)^2\right]-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left[\left(x+1\right)^2+\left(x^2-1\right)+\left(x-1\right)^2\right]-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left[\left(x^2+2x+1\right)+\left(x^2-1\right)+\left(x^2-2x+1\right)\right]-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left(x^2+2x+1+x^2-1+x^2-2x+1\right)-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left(3x^2+1\right)-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow6x^2+2-6\left(x^2-2x+1\right)=-10\)
\(\Leftrightarrow6x^2+2-6x^2+12x-6=-10\)
\(\Leftrightarrow12x-4=-10\)
\(\Leftrightarrow12x=-6\)
\(\Leftrightarrow x=-\dfrac{6}{12}=-\dfrac{1}{2}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
30 tháng 6 2023
\(a,\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=1\\ \Leftrightarrow x^3-3x^2+3x^2-9x+9x-27+\left(x^2+2x\right)\left(2-x\right)-1=0\\ \Leftrightarrow x^3-3x^2+3x^2-9x+9x-27+2x^2-x^3+4x-2x^2-1=0\\ \Leftrightarrow x^3-x^3-3x^2+3x^2+2x^2-2x^2-9x+9x+4x=1+27\\ \Leftrightarrow4x=28\\ \Leftrightarrow x=7\)
A
23 tháng 6 2023
\(a,3\left(2a-1\right)+5\left(3-a\right)\)
\(=6a-3+15-5a\)
\(=a-12\)
Thay \(a=\dfrac{-3}{2}\) vào biểu thức trên
\(a-12\)
\(=\dfrac{-3}{2}-12\)
\(=\dfrac{-27}{2}\)
\(b,25x-4\left(3x-1\right)+7\left(5-2x\right)\)
\(=25x-12x+4+35-14x\)
\(=-1x+39\)
Thay \(x=2,1\) vào biểu thức trên
\(-1x+39\)
\(=-1.2,1+39\)
\(=-2,1+39\)
\(=36,9\)
\(c,4a-2\left(10a-1\right)+8a-2\)
\(=4a-20a+2+8a-2\)
\(=-8a\)
Thay \(a=-0,2\) vào biểu thức trên
\(-8a\)
\(=-8.\left(-0,2\right)\)
\(=1,6\)
\(d,12\left(2-3b\right)+35b-9\left(b+1\right)\)
\(=24-36b+35b-9b-9\)
\(=-10b-15\)
Thay \(b=\dfrac{1}{2}\) vào biểu thức trên
\(-10b-15\)
\(=-10.\dfrac{1}{2}-15\)
\(=-20\)
23 tháng 6 2023
a: =6y^3-3y^2-y^2+2y-y+y^2-y^3
=5y^3-3y^2+y
b: =2x^2a-a-2x^2a-a-x^2-ax
=-x^2-ax-2a
c: =2p^3-p^3+1+2p^3+6p^2-3p^5
=3p^3+6p^2-3p^5+1
d: =-3a^3+5a^2+4a^3-4a^2=a^3+a^2
AH
Akai Haruma
Giáo viên
29 tháng 6 2023
d.
$(\frac{x}{2}-y)^3=(\frac{x}{2})^3-3(\frac{x}{2})^2y+3.\frac{x}{2}y^2-y^3$
$=\frac{x^3}{8}-\frac{3x^2y}{4}+\frac{3xy^2}{2}-y^3$
e.
$(\frac{x}{2}+\frac{y}{3})^3=(\frac{x}{2})^3+3(\frac{x}{2})^2\frac{y}{3}+3.\frac{x}{2}(\frac{y}{3})^2+(\frac{y}{3})^3$
$=\frac{x^3}{8}+\frac{x^2y}{4}+\frac{xy^2}{6}+\frac{y^3}{27}$
f.
$(\frac{2x}{3}-2y)^3=(\frac{2x}{3})^3-3(\frac{2x}{3})^2.2y+3.\frac{2x}{3}(2y)^2-(2y)^3$
$=\frac{8x^3}{27}-\frac{8x^2y}{3}+8xy^2-8y^3$
g.
$(x+y)^3+(x-y)^3=(x^3+3x^2y+3xy^2+y^3)+(x^3-3x^2y+3xy^2-y^3)$
$=2x^3+6xy^2$
AH
Akai Haruma
Giáo viên
29 tháng 6 2023
Lời giải:
a.
$(3-y)^3=3^3-3.3^2y+3.3y^2-Y63=27-27y+9y^2-y^3$
b.
$(3x+2y^2)^3=(3x)^3+3.(3x)^2(2y^2)+3.3x(2y^2)^2+(2y^2)^3$
$=8y^6+24xy^4+24x^2y^2+8x^3$
c.
$(x-3y^2)^3=x^3-3x^2(3y^2)+3x(3y^2)^2-(3y^2)^3$
$=x^3-9x^2y^2+27xy^4-27y^6$
Y
29 tháng 6 2023
\(a,-x^3+3x^2-3x+1=-\left(x^3-3x^2+3x-1\right)=-\left(x-1\right)^3\)
\(b,8-12x+6x^2-x^3=2^3-3.2^2x+3.2x^2-x^3=\left(2-x\right)^3\)
\(c,x^3-6x^2y+12xy^2-8y^3=x^3-3.2y.x^2+2.\left(2y\right)^2x-\left(2y\right)^3=\left(x-2y\right)^3\)
\(d,8x^3+12x^2+6x+1\\ =\left(2x\right)^3+3.1\left(2x\right)^2+3.2x.1^2+1^3=\left(2x+1\right)^3\)
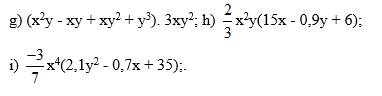
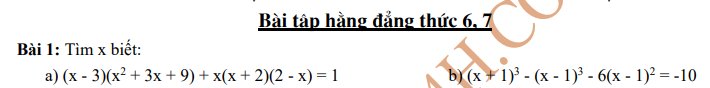
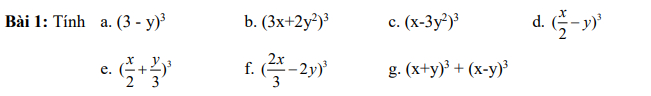
\(g,\left(x^2y-xy+xy^2+y^3\right).3xy^2\\ =\left(3xy^2.x^2y\right)-\left(3xy^2.xy\right)+\left(3xy^2.xy^2\right)+\left(3xy^2.y^3\right)\\ =3x^3y^3-3x^2y^3+3x^2y^4+3xy^5\)
\(h,\dfrac{2}{3}x^2y\left(15x-0,9y+6\right)\\ =\left(\dfrac{2}{3}x^2y.15x\right)-\left(\dfrac{2}{3}x^2y.0,9y\right)+\left(\dfrac{2}{3}x^2y.6\right)\\ =10x^3y-\dfrac{3}{5}x^2y^2+4x^2y\)
\(i,-\dfrac{3}{7}x^4\left(2,1y^2-0,7x+35\right)\\ =\left(-\dfrac{3}{7}x^4.2,1y^2\right)-\left(-\dfrac{3}{7}x^4.0,7x\right)+\left(-\dfrac{3}{7}x^4.35\right)\\ =-\dfrac{9}{10}x^4y^2+\dfrac{3}{10}x^5-15x^4\)
g: =x^2y*3xy^2-xy*3xy^2+xy^2*3xy^2+y^3*3xy^2
=3x^3y^3-3x^2y^3+3x^2y^4+3xy^5
h: =2/3x^2y*15x-2/3x^2y*0,9y+2/3x^2y*6
=10x^3y-0,6x^2y^2+4x^2y
i: =-3/7x^4*2,1y^2+3/7x^4*0,7x-3/7x^4*35
=-0,9x^4y^2+3/10x^5-15x^4