
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên

29 tháng 12 2021
b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)

30 tháng 6 2023
1: góc AHC+góc AKC=180 độ
=>AHCK nội tiếp
2: AHCK nội tiếp
=>góc AHK=góc ACK=1/2*sđ cung AC=góc ABC

22 tháng 12 2022
BH=12^2/9=16cm
BC=16+9=25cm
AB=căn(16*25)=20cm
AC=căn(9*25)=15cm
sin B=AC/BC=3/5
tan C=AB/AC=20/15=4/3

23 tháng 6 2023
ΔCAD vuông tại C có CH là đường cao
nên AH*HD=CH^2
ΔABC vuông tại A có AH là đường cao
nên BH*HC=AH^2
AH*HD+BH*HC=CH^2+AH^2=CA^2
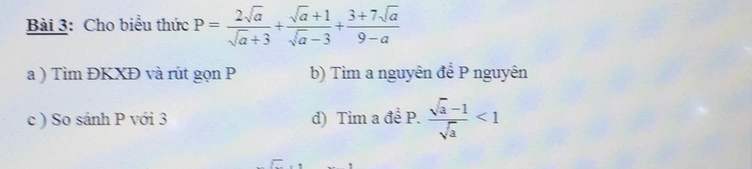



a, đkxđ : a >= 0 ; a khác 9
\(P=\dfrac{2\sqrt{a}\left(\sqrt{a}-3\right)+\left(\sqrt{a}+1\right)\left(\sqrt{a}+3\right)-3-7\sqrt{a}}{a-9}\)
\(=\dfrac{2a-6\sqrt{a}+a+4\sqrt{a}+3-3-7\sqrt{a}}{a-9}=\dfrac{3a-9\sqrt{a}}{a-9}=\dfrac{3\sqrt{a}}{\sqrt{a}+3}\)
b, \(\dfrac{3\sqrt{a}}{\sqrt{a}+3}=\dfrac{3\left(\sqrt{a}+3\right)-9}{\sqrt{a}+3}=3-\dfrac{9}{\sqrt{a}+3}\Rightarrow\sqrt{a}+3\inƯ\left(9\right)=\left\{1;3;9\right\}\)
c, Ta có : \(3=\dfrac{3\left(\sqrt{a}+3\right)}{\sqrt{a}+3}\)mà \(3\left(\sqrt{a}+3\right)>3\sqrt{a}\)
Vậy P < 3
d, Ta có : \(\dfrac{3\sqrt{a}}{\sqrt{a}+3}.\dfrac{\sqrt{a}-1}{\sqrt{a}}< 1\Leftrightarrow\dfrac{3\left(\sqrt{a}-1\right)}{\sqrt{a}+3}-1< 0\)
\(\Leftrightarrow\dfrac{3\sqrt{a}-3-\sqrt{a}-6}{\sqrt{a}+3}< 0\Rightarrow2\sqrt{a}-9< 0\)vì \(\sqrt{a}+3>0\)
\(\Leftrightarrow\sqrt{a}< \dfrac{9}{2}\Leftrightarrow a< \dfrac{81}{4}\)
Kết hợp đk vậy \(0\le a< \dfrac{81}{4}\)