K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PN
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
0
TQ
5
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
17 tháng 7 2021
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
3 tháng 1 2022
b: \(A=\dfrac{\sqrt{x}-\sqrt{x}+1}{x-1}\cdot\dfrac{x-1}{\sqrt{x}-1}=\dfrac{1}{\sqrt{x}-1}\)
12 tháng 5 2023
4:
Gọi chiều rộng là x
=>Chiều dài là 4x
=>Diện tích là 4x^2
Theo đề, ta có: (x-2)*8x=4x^2+20
=>8x^2-16x-4x^2-20=0
=>x^2-4x-5=0
=>x=5
=>S=4*5^2=100m2
Số tiền của mảnh vườn là:
100*20000000=2000000000(đồng)
M
1
2 tháng 10 2021
\(P=\dfrac{2\sqrt{x}+1+\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+1+1-x}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{-x+2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}=\dfrac{-x+2\sqrt{x}+2}{x+3\sqrt{x}+2}\)
NP
0
19 tháng 7 2021
a) Ta có: \(\sqrt{\dfrac{a}{b}}+\sqrt{ab}+\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}\)
\(=\dfrac{\sqrt{ab}}{b}+\sqrt{ab}+\dfrac{a}{b}\cdot\dfrac{\sqrt{b}}{\sqrt{a}}\)
\(=\dfrac{\sqrt{ab}}{b}+\dfrac{b\sqrt{ab}}{b}+\dfrac{\sqrt{ab}}{b}\)
\(=\dfrac{b\sqrt{ab}+2\sqrt{ab}}{b}\)
b) \(\sqrt{\dfrac{m}{x^2-2x+1}}\cdot\sqrt{\dfrac{4mx^2-8mx+4m}{81}}\)
\(=\sqrt{\dfrac{m}{\left(x-1\right)^2}\cdot\dfrac{4m\left(x-1\right)^2}{81}}\)
\(=\sqrt{\dfrac{4m^2}{81}}=\dfrac{2m}{9}\)
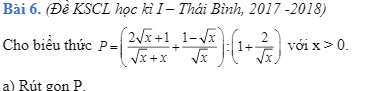
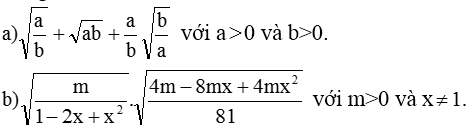
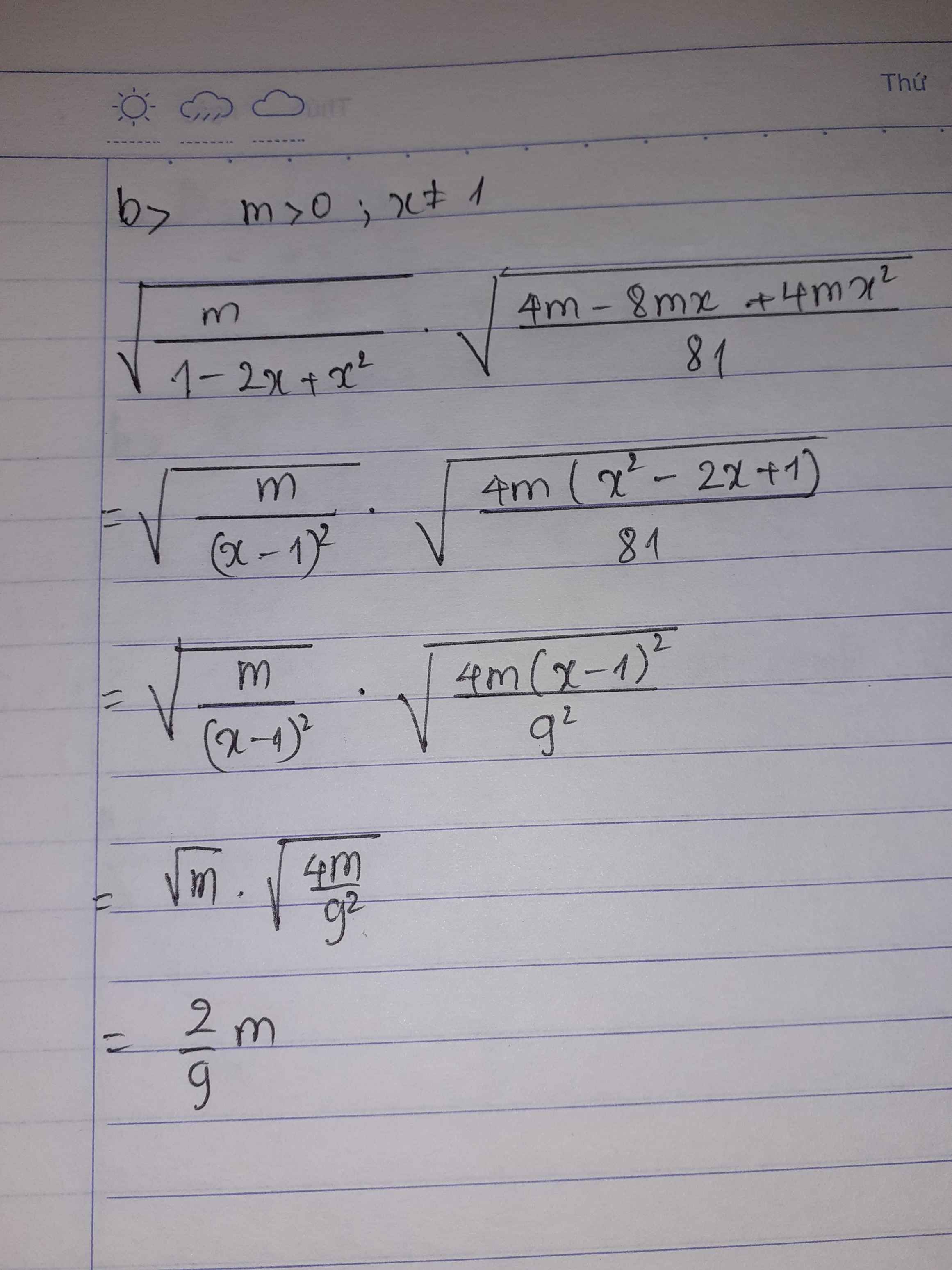
b: Xét ΔAEB vuông tại E và ΔAKC vuông tại K có
\(\widehat{EAB}\) chung
Do đó: ΔAEB\(\sim\)ΔAKC
Suy ra: \(\dfrac{AE}{AK}=\dfrac{AB}{AC}\)
hay \(AK\cdot AB=AE\cdot AC\)