K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CB
10
5 tháng 12 2021
\(a,49-\left(6^2-18:3^2\right)=49-\left(36-18:9\right)=49-\left(36-2\right)=49-34=15\\ b,320+\left[148-\left(5^2-3.5\right)^2\right]=320+\left[148-\left(25-15\right)^2\right]=320+\left(148-10^2\right)=320+\left(148-100\right)=320+48=368\)
14 tháng 11 2018
Vì UCLN(a,b)=30 nên ta đặt a=30c, b=30d (c,d thuộc N và c<d,UCLN(c, d) =1)
Ta có a+b=30c+30d=240=>c+d=8.
Vì UCLN(c,d)= 1 và c<d nên ta có 2 trường hợp :
c=7, d=1 suy ra a=210, b=30
c=5, d=3 suy ra a=150, b=90.
Chúc bạn học tốt!
Kb vs mình nha
KT
20 tháng 1 2018
\(\frac{7}{25}+\frac{-18}{25}+\frac{4}{23}+\frac{5}{7}+\frac{19}{23}\)
\(=\left(\frac{7}{25}-\frac{11}{25}\right)+\left(\frac{4}{23}+\frac{19}{23}\right)+\frac{5}{7}\)
\(=\frac{-4}{25}+1+\frac{5}{7}\)
\(=\frac{-28}{175}+\frac{175}{175}+\frac{125}{175}\)
\(=\frac{272}{175}\)
🤔
HH
10 tháng 8 2017
Ta có: \(\dfrac{1}{299}+\dfrac{4}{299}+\dfrac{7}{299}+...+\dfrac{298}{299}\) \(=\dfrac{1+4+7+...+298}{299}\)
Tính riêng mãu ta được: \(1+4+7+...+298=\dfrac{\left[\left(298-1\right):3+1\right].\left(298+1\right)}{2}\)
\(=14950\)
Ghép vào vs mẫu ta được: \(\dfrac{14950}{299}\) \(=50\)
Vậy \(\dfrac{1}{299}+\dfrac{4}{299}+\dfrac{7}{299}+...+\dfrac{298}{299}=50\).
MV
10 tháng 8 2017
rối mắt quá nhá
\(\dfrac{1}{299}+\dfrac{4}{299}+\dfrac{7}{299}+...+\dfrac{298}{299}\\ =\dfrac{1+4+7+...+298}{299}\\ =\dfrac{\left(\dfrac{298-1}{3}+1\right)\cdot\left(298+1\right)}{2}:299\\ =\dfrac{100\cdot299}{2}\cdot\dfrac{1}{299}\\ =\dfrac{100\cdot299}{2\cdot299}\\ =50\)
8 tháng 10 2020
Nhờ thì nói luôn đi, đố cái gì-.-
a) Ta có: \(S=1+2+...+2^{59}\)
\(\Rightarrow2S=2+2^2+...+2^{60}\)
\(\Rightarrow2S-S=\left(2+2^2+...+2^{60}\right)-\left(1+2+...+2^{59}\right)\)
\(\Leftrightarrow S=2^{60}-1< 2^{60}\)
b) Ta có: \(S=1+2+2^2+2^3+...+2^{59}\)
\(S=\left(1+2+2^2\right)+\left(2^3+2^4+2^5\right)+...+\left(2^{57}+2^{58}+2^{59}\right)\)
\(S=7+2^3\cdot7+...+2^{57}\cdot7\)
\(S=7\cdot\left(1+2^3+...+2^{57}\right)\) chia hết cho 7
8 tháng 10 2020
theo mik thì bạn phải tách ra là S = 1+2+2^2+2^3+2^4+2^5+2^7 chứ ???
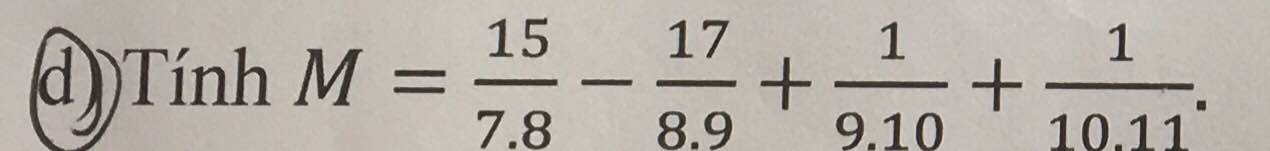
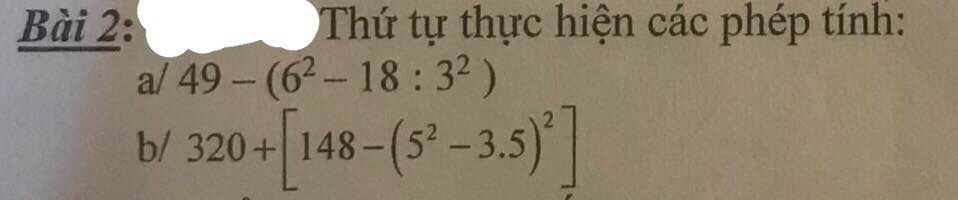
=1/7+1/8-1/8-1/9+1/9-1/10+1/10-1/11
=1/7-1/11
=4/77