
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc ACB=1/2*sđ cung AB=90 độ
góc BCE+góc BDE=180 độ
=>BCED nội tiếp
góc ADF=góc ACF=90 độ
=>ADCF nội tiếp
b: góc GEC=góc AED=góc ABC=1/2*sđ cung AC
góc GCE=1/2*sđ cung CA
=>góc GEC=góc GCE
=>ΔGEC cân tại G


a: góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: góc EAH=90 độ-goc ABC
góc ECB=90 độ-góc ABC
=>góc EAH=góc ECB
c: góc xAC=góc ABC
=>góc xAC=góc ADE
=>xy//DE

Bài 5:
a: Xét (O) có
ΔDMN nội tiếp
MN là đường kính
Do đó: ΔDMN vuông tại D


Bài 1:
\(a,x=3;y=\sqrt{10\cdot1,2}=\sqrt{12}=2\sqrt{3};z=\dfrac{\sqrt{5}\left(2\sqrt{3}-1\right)}{\sqrt{5}}=2\sqrt{3}-1\)
Ta có \(2\sqrt{3}-1=\sqrt{12}-1< \sqrt{16}-1=3\Leftrightarrow z< x\left(1\right)\)
Mà \(3=\sqrt{9}< \sqrt{12}=2\sqrt{3}\Leftrightarrow x< y\left(2\right)\)
\(\left(1\right)\left(2\right)\Leftrightarrow z< x< y\)
\(b,\Leftrightarrow3\left(\sin^2\alpha+\cos^2\alpha\right)+2\cos^2\alpha=4,5\\ \Leftrightarrow3\cdot1+2\cos^2\alpha=4,5\\ \Leftrightarrow\cos^2\alpha=\dfrac{3}{4}\Leftrightarrow\cos\alpha=\dfrac{\sqrt{3}}{2}\\ \Leftrightarrow\alpha=30^0\)
Câu 2:
\(a,ĐK:x\ge-2\\ BPT\Leftrightarrow3\sqrt{x+2}-\sqrt{x+2}+\sqrt{x+2}< 12\\ \Leftrightarrow3\sqrt{x+2}< 12\\ \Leftrightarrow x+2< 16\Leftrightarrow x< 14\\ \Leftrightarrow-2\le x< 14\)
Vậy BPT có vsn trong khoảng \([-2;14)\)
\(b,HPT\Leftrightarrow\left\{{}\begin{matrix}3x-2y=7\\5x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x=8\\3x-2y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Câu 3:
\(a,A=\dfrac{x+\sqrt{x}+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{2}-2\sqrt{\dfrac{x\left(x-3\right)}{x}}\\ A=\dfrac{2x}{2}-2\sqrt{x-3}=x-2\sqrt{x-3}\\ x=7+2\sqrt{3}\Leftrightarrow A=7+2\sqrt{3}-2\sqrt{4+2\sqrt{3}}=7+2\sqrt{3}-2\left(\sqrt{3}+1\right)=5\)
\(b,A=x-2\sqrt{x-3}=x-3-2\sqrt{x-3}+1+2\\ A=\left(\sqrt{x-3}-1\right)^2+2\ge2\)
Dấu \("="\Leftrightarrow\sqrt{x-3}=1\Leftrightarrow x-3=1\Leftrightarrow x=4\left(tm\right)\)

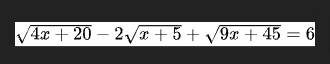



 giải giúp mình với ạ
giải giúp mình với ạ Giúp mình câu 4,5 với ạ
Giúp mình câu 4,5 với ạ 

\(\sqrt{4x+20}-2\sqrt{x+5}+\sqrt{9x+45}=6\left(đk:x\ge-5\right)\)
\(\Leftrightarrow2\sqrt{x+5}-2\sqrt{x+5}+3\sqrt{x+5}=6\)
\(\Leftrightarrow3\sqrt{x+5}=6\)
\(\Leftrightarrow\sqrt{x+5}=2\Leftrightarrow x+5=4\Leftrightarrow x=-1\left(tm\right)\)
\(\sqrt{4x+20}-2\sqrt{x+5}+\sqrt{9x+45}=6\) ĐK: \(x\ge5\)
<=> \(\sqrt{4\left(x+5\right)}-2\sqrt{x+5}+\sqrt{9\left(x+5\right)}=6\)
<=> \(2\sqrt{x+5}-2\sqrt{x+5}+3\sqrt{x+5}=6\)
<=> \(3\sqrt{x+5}=6\)
<=> \(\sqrt{x+5}=6:3\)
<=> \(\sqrt{x+5}=2\)
<=> x + 5 = 22
<=> x + 5 = 4
<=> x = 4 - 5
<=> x = -1 (loại)
Vậy nghiệm của PT là \(S=\varnothing\)