
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





\(a,\Rightarrow20\cdot2^x=160+1-1\\ \Rightarrow2^x=160:20=8=2^3\\ \Rightarrow x=3\\ b,\Rightarrow\left(4-x:2\right)^3=2\left(8-5\right)+1+1\\ \Rightarrow\left(4-x:2\right)^3=6+2=8=2^3\\ \Rightarrow4-x:2=2\\ \Rightarrow x:2=2\Rightarrow x=4\\ c,n\left(n+2017\right)\)
Với n chẵn thì \(n=2k\left(k\in N\right)\Rightarrow n\left(n+2017\right)=2k\left(n+2017\right)⋮2\)
Với n lẻ thì \(n=2k+1\left(k\in N\right)\Rightarrow n\left(n+2017\right)=n\left(2k+2018\right)=2n\left(k+1009\right)⋮2\)
Vậy \(n\left(n+2017\right)\) luôn chẵn
\(d,3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}=\left(2^3\right)^{100}=2^{300}\)

O1=O2( vì 2 góc đối đỉnh)
O3 và O4 thì làm theo cách hai góc kề bù
Vd :O1+O3=180 độ (2 góc kề bù)
Suy ra :120 độ +O3=180 độ
Vậy từ đó tính ra đc O3 ,tương tự O4 cũng vậy

(2.x-4). (x-1)=0
Số nào nhân với 0 cx bằng 0
TH1: 2.x-4=0. TH2: x-1=0
2x=0+4. x=0+1
2x=4. x=1
x=4÷2
x=2
\(\left(2x-4\right)\cdot\left(x-1\right)=0\Rightarrow\left(2x^2-6x+4\right)=0\Leftrightarrow\left(2x-4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-4=0\\x-1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=1\end{cases}}\)
ủng hộ mik nha

Khoảng cách có rồi thì bạn áp dụng công thức : \(\frac{a}{m.n}=\frac{1}{m}-\frac{1}{n}\)(với n-m=a) là làm được
S=\(\frac{2}{5.7}+\frac{2}{7.9}+...+\frac{2}{93.95}+\frac{3}{95.98}+\frac{4}{98.102}+\frac{5}{102.17}+\frac{2012}{107..2119}\)
S=\(\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+...+\frac{1}{93}-\frac{1}{95}+\frac{1}{95}-\frac{1}{98}+\frac{1}{98}-\frac{1}{102}+\frac{1}{102}-\frac{1}{107}+\frac{1}{107}-\frac{1}{2119}\)
S=\(\frac{1}{5}-\frac{1}{2119}\)
S=\(\frac{2114}{10595}\)

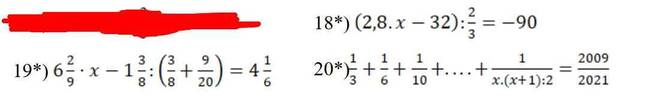
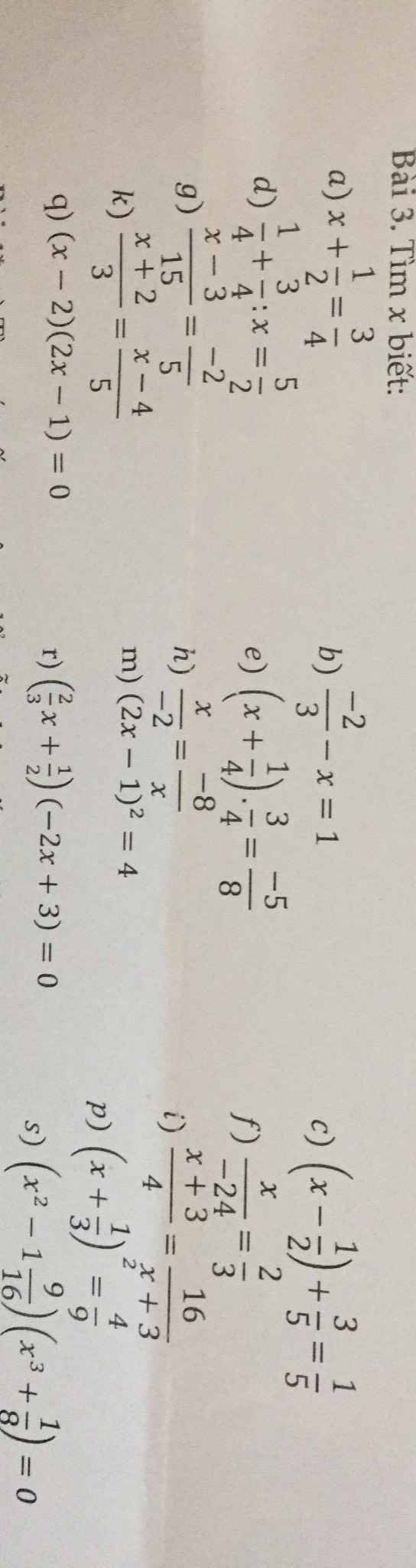
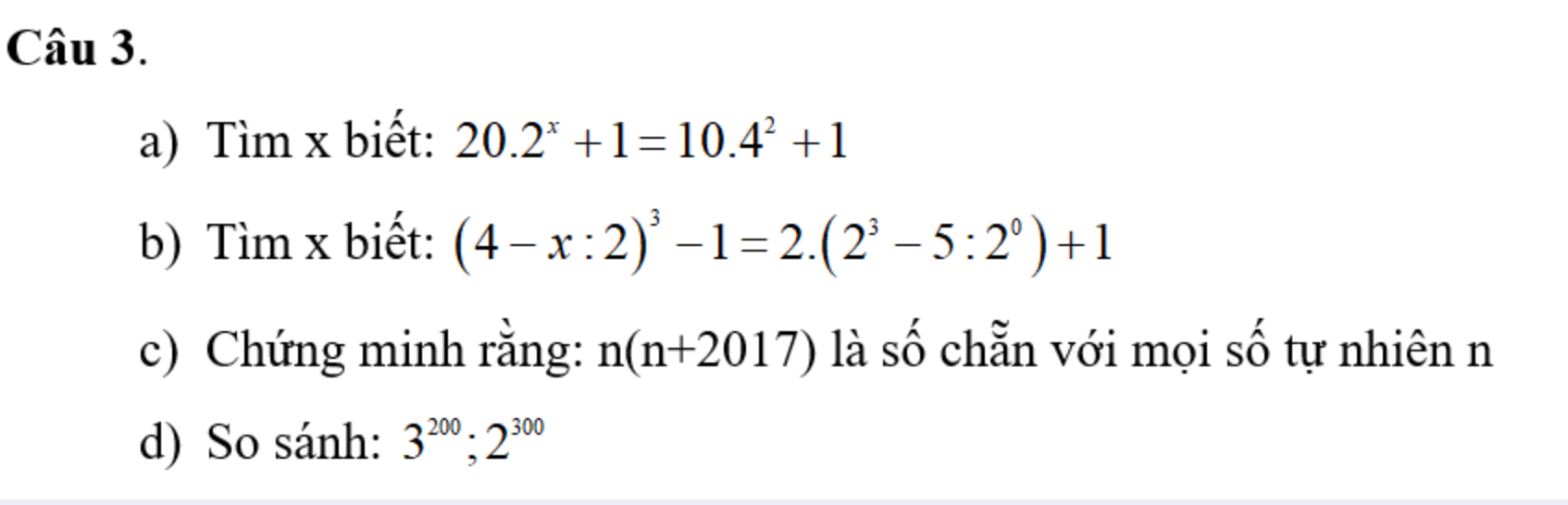 giúp mình với, mình cần gấp lắm, 5p phải nộp rồi
giúp mình với, mình cần gấp lắm, 5p phải nộp rồi


Bài 3.85:
6/35=2/5:7/3
Bài 3.86
a: \(A=\dfrac{2\left(\dfrac{1}{7}+\dfrac{1}{5}+\dfrac{1}{17}-\dfrac{1}{293}\right)}{3\left(\dfrac{1}{7}+\dfrac{1}{5}+\dfrac{1}{17}-\dfrac{1}{293}\right)}=\dfrac{2}{3}\)
b: \(B=\left(\dfrac{7}{12}+\dfrac{10}{12}-\dfrac{12}{12}\right):\left(\dfrac{60}{12}-\dfrac{9}{12}+\dfrac{4}{12}\right)=\dfrac{5}{12}\cdot\dfrac{12}{55}=\dfrac{1}{11}\)