
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



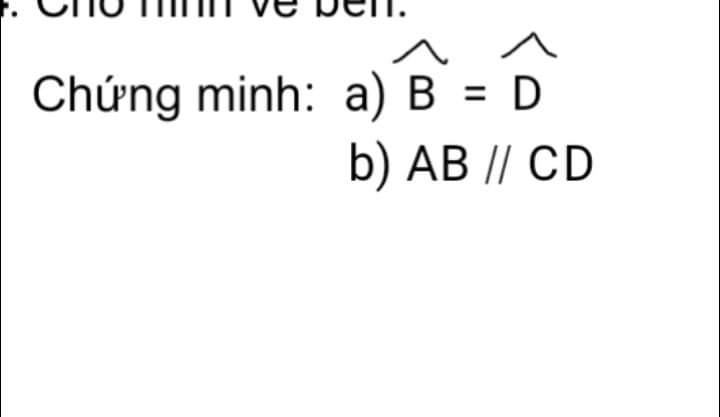
a: Xét ΔABE và ΔADC có
AB=AD
\(\widehat{BAE}=\widehat{DAC}\)
AE=AC
Do đó: ΔABE=ΔADC


Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a-3b}{2\cdot5-3\cdot2}=\dfrac{12}{4}=3\)
Do đó: a=15; b=6
d) Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a}{10}=\dfrac{3b}{6}=\dfrac{2a-3b}{10-6}=\dfrac{12}{4}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=3.5=15\\b=3.2=6\end{matrix}\right.\)
f) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}=-\dfrac{z}{2}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{-z}{2}=\dfrac{x+y-z}{5+3+2}=\dfrac{2}{10}=\dfrac{1}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}.5=1\\y=\dfrac{1}{5}.3=\dfrac{3}{5}\\z=\dfrac{1}{5}.\left(-2\right)=-\dfrac{2}{5}\end{matrix}\right.\)
g) \(\dfrac{x}{4}=\dfrac{y}{5}=k\)\(\Rightarrow\left\{{}\begin{matrix}x=4k\\y=5k\end{matrix}\right.\)
\(\Rightarrow xy=20k^2=500\Rightarrow k=\pm5\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\\\left\{{}\begin{matrix}x=-20\\y=-25\end{matrix}\right.\end{matrix}\right.\)

Bài 1 :
Thay x = 2 ; y = -1/2 ta được
\(B=-8+2.4\left(-\dfrac{1}{2}\right)-4.2.\left(\dfrac{1}{4}\right)+2\left(-\dfrac{1}{2}\right)-3\)
\(=-8-4-2-1-3=-18\)

a: \(P=-\left|5-x\right|+2019\le2019\forall x\)
Dấu '=' xảy ra khi x=5


Bài 1:
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
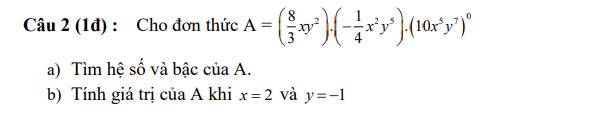 giúp mình với, mình cảm ơn nhiều
giúp mình với, mình cảm ơn nhiều

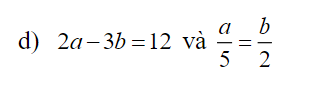
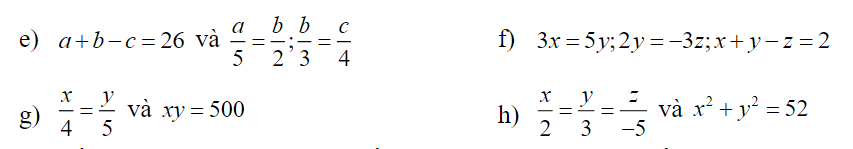
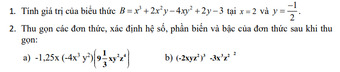

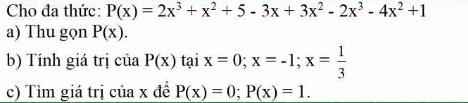

a, \(A=\left(\dfrac{8}{3}xy^2\right).\left(\dfrac{-1}{4}x^2y^5\right).\left(10x^5y^7\right)^0\)
⇒\(A=\dfrac{8}{3}xy^2.\dfrac{-1}{4}x^2y^5.1\)
⇒\(A=\left(\dfrac{8}{3}.\dfrac{-1}{4}.1\right).\left(x.x^2\right).\left(y^2.y^5\right)\)
⇒\(A=\dfrac{-2}{3}x^3y^7\)
+)Hệ số: \(\dfrac{-2}{3}\)
+)Bậc:10
b, Thay \(x=2\), \(y=-1\) vào A ta có:
\(A=\dfrac{-2}{3}.2^3.\left(-1\right)^7\)
⇒\(A=\dfrac{-2}{3}.8.\left(-1\right)\)
⇒\(A=\dfrac{16}{3}\)
Vậy \(A=\dfrac{16}{3}\) khi \(x=2,y=-1\)