K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 9 2021
a: Theo đề, ta có:
BH+CH=25(cm)
hay BH=25-CH
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC\left(HC-25\right)=-144\)
\(\Leftrightarrow HC=16\left(cm\right)\)
\(\Leftrightarrow HB=9\left(cm\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{9\cdot25}=15\left(cm\right)\\AC=\sqrt{16\cdot25}=20\left(cm\right)\end{matrix}\right.\)
giúp mình với ạ mình cảm ơn nhiều
5 tháng 11 2021
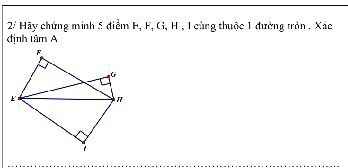
Bài 1:
Xét tứ giác ABDC có \(\widehat{A}+\widehat{D}=180^0\)
nên ABDC là tứ giác nội tiếp
7 tháng 1 2022
a: Đặt 1/x=a
1/(y-2)=b
Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}2a+3b=4\\4a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+6b=8\\4a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=7\\4a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{7}{5}\\a=-\dfrac{1}{10}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{-1}{10}\\\dfrac{1}{y-2}=\dfrac{7}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-10\\y-2=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-10\\y=\dfrac{19}{7}\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{2}{y}=0\\\dfrac{2}{x+1}+\dfrac{3}{y}=-1\end{matrix}\right.\)
=>Hệ phương trình vô nghiệm
7 tháng 1 2022
a) \(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y-2}=4.\\\dfrac{4}{x}+\dfrac{1}{y-2}=1.\end{matrix}\right.\) \(ĐK:x\ne0;y\ne2.\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y-2}=b\left(a;b\ne0\right).\)
\(\Rightarrow\left\{{}\begin{matrix}2a+3b=4.\\4a+b=1.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-1}{10}.\\b=\dfrac{7}{5}.\end{matrix}\right.\) (TM).
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{-1}{10}.\\\dfrac{1}{y-2}=\dfrac{7}{5}.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-10\left(TM\right).\\y=\dfrac{19}{7}\left(TM\right).\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm \(\left(x;y\right)=\left(-10;\dfrac{19}{7}\right).\)
17 tháng 10 2021
Bài 1:
a: \(\dfrac{13\sqrt{2}-4\sqrt{6}}{24-4\sqrt{3}}=\dfrac{\sqrt{2}\left(13-4\sqrt{3}\right)}{4\sqrt{3}\left(2\sqrt{3}-1\right)}=\dfrac{\sqrt{2}\left(2\sqrt{3}-1\right)}{4\sqrt{3}}=\dfrac{\sqrt{6}\left(2\sqrt{3}-1\right)}{12}\)
b: \(\dfrac{\sqrt{3-2\sqrt{2}}}{\sqrt{17-12\sqrt{2}}}=\dfrac{\sqrt{2}-1}{3-2\sqrt{2}}=\sqrt{2}+1\)
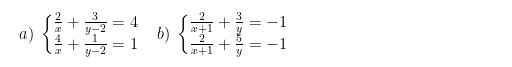
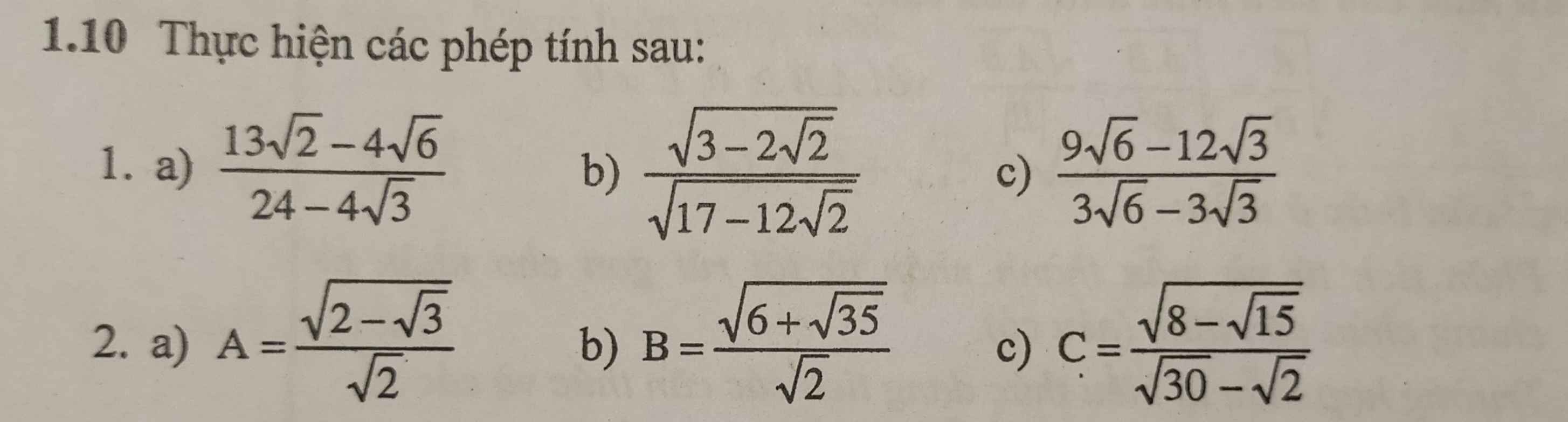
Bài 2 :
a, \(\sqrt{4a^2}+5a\)với a >= 0
\(=\left|2a\right|+5a=7a\)
b, \(\sqrt{25x^2}+3x=\left|5x\right|+3x=-5x+3x=-2x\)với x =< 0
c, \(x-2-\sqrt{4-4x+x^2}=x-2-\sqrt{\left(2-x\right)^2}=x-2-\left|2-x\right|\)
\(=x-2-2+x=-4\)với x =< 2
d, \(3-x+\sqrt{9+9x+x^2}=3-x+\sqrt{\left(3+x\right)^2}=3-x+\left|x+3\right|\)
\(=3-x+x+3=6\)với x =< -3
BẠn viết ra giấy đc ko mình ko nhìn thấy