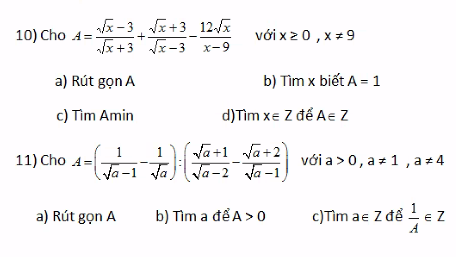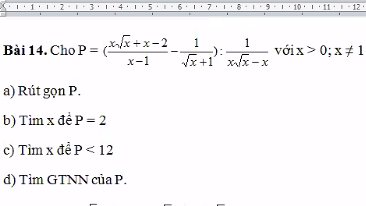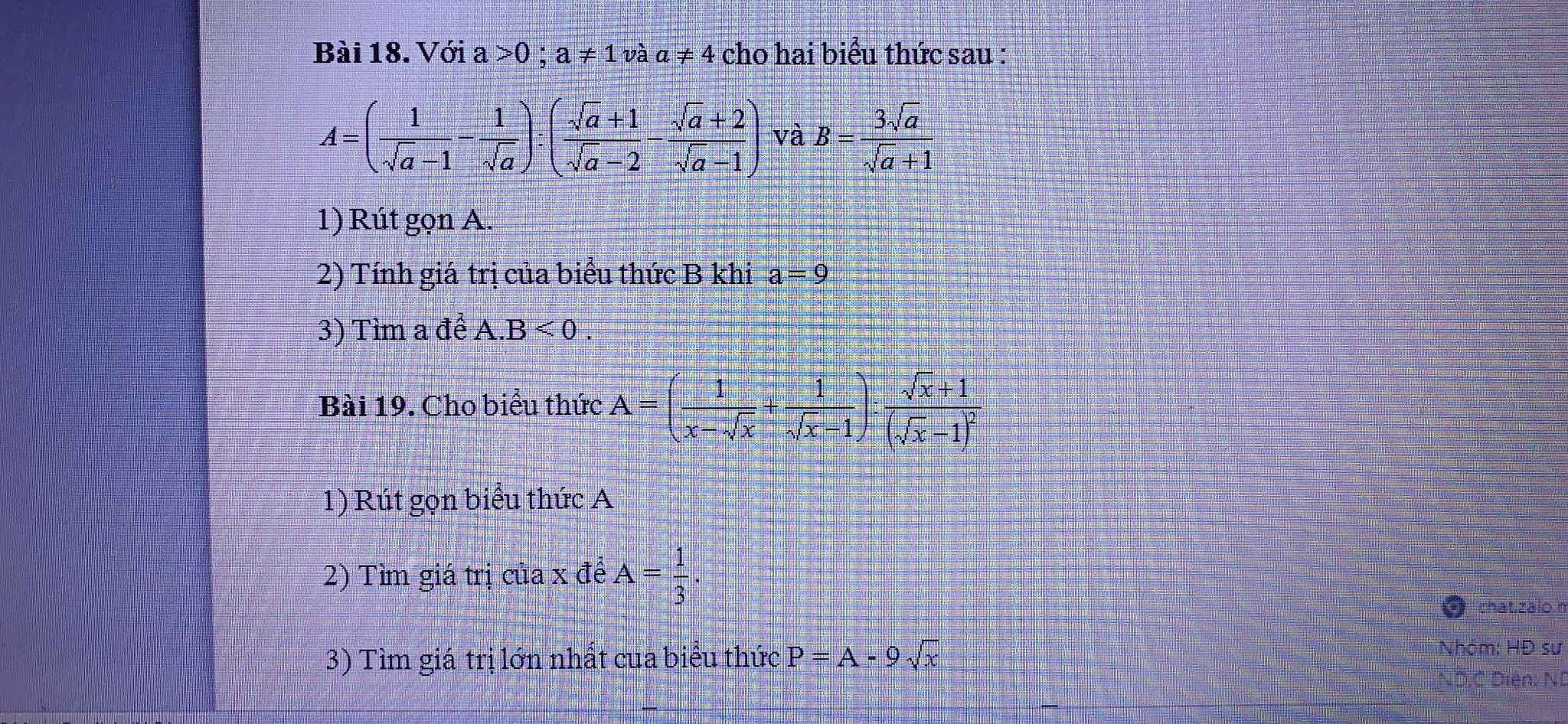CH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 7 2021
a) P rút gọn lại là = x(x-1)
b) Để P = 2 => \(x^2\)- x -2 = 0
=> x = 2 hay x = -1
c) Để P<12 => \(x^2\) - x -12< 0
=> (x-4)(x+3) <0
=> x-4 <0<x+3
=> x<4 hay x >-3
Vậy, -3<x<4 thì P<12
d) GTNN của P = \(x^2\)- x
= \(x^2\)- x +1/4 -1/4
= (x-1/2)\(^2\)-1/4 >= -1/4
Vậy, GTNN của x là -1/4 khi và chỉ khi x = 1/2
Nhớ like giúp mik nha bạn. Thx bạn nhìu:33
22 tháng 7 2021
a) Ta có: \(P=\left(\dfrac{x\sqrt{x}+x-2}{x-1}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{1}{x\sqrt{x}-x}\)
\(=\dfrac{x\sqrt{x}+x-2-\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{x\left(\sqrt{x}-1\right)}{1}\)
\(=\dfrac{x\sqrt{x}+x-\sqrt{x}-1}{\sqrt{x}+1}\cdot x\)
\(=\dfrac{x\left(\sqrt{x}+1\right)-\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\cdot x\)
\(=x^2-x\)
CH
4
AH
Akai Haruma
Giáo viên
16 tháng 8 2021
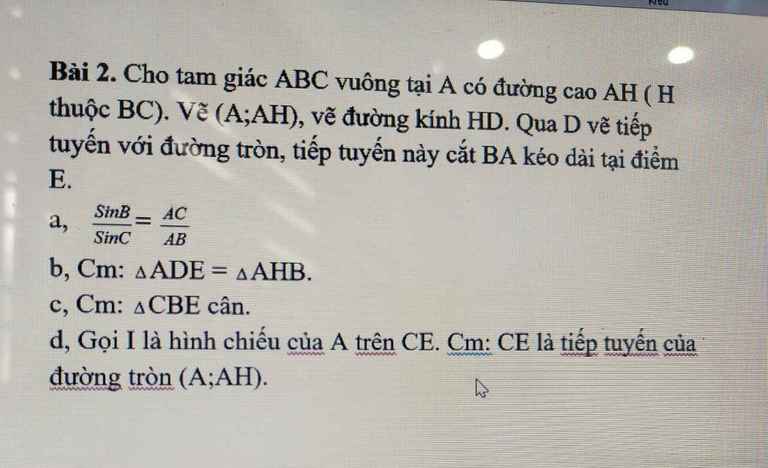
Bài 2:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{4^2-2,4^2}=3,2$ (cm)
b.
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=9.16$
$\Rightarrow AH=12$ (cm)
Áp dụng định lý Pitago:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
$BC=BH+CH=9+16=25$ (cm)
AH
Akai Haruma
Giáo viên
16 tháng 8 2021
Bài 3:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ (cm)
Áp dụng định lý Pitago:
$15=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$
$\Rightarrow a=3$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{3a.4a}{5a}=2,4a$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(3a)^2-(2,4a)^2}=1,8a=1,8.3=5,4$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-(2,4a)^2}=3,2a=3,2.3=9,6$ (cm)
TH
1
16 tháng 6 2023
2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40
2 tháng 9 2021
a: Xét ΔABH vuông tại H có HF là đường cao ứng với cạnh huyền AB
nên \(AF\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
20 tháng 6 2023
3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8
AH
0
25 tháng 7 2021
Bài 18
a, Với \(a>0;a\ne1;4\)
\(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\left(\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{3}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
b, Thay a = 9 => căn a = 3
\(A=\dfrac{3-2}{3.3}=\dfrac{1}{9}\)
c, Ta có : \(A.B=\dfrac{\sqrt{a}-2}{3\sqrt{a}}.\dfrac{3\sqrt{a}}{\sqrt{a}+1}=\dfrac{\sqrt{a}-2}{\sqrt{a}+1}< 0\)
Vì \(\sqrt{a}+1>\sqrt{a}-2\)
\(\left\{{}\begin{matrix}\sqrt{a}+1>0\\\sqrt{a}-2< 0\end{matrix}\right.\Leftrightarrow a< 4\)
Kết hợp với đk vậy \(0< a< 4;a\ne1\)
25 tháng 7 2021
Bài 18:
1) Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
2) Thay a=9 vào B, ta được:
\(B=\dfrac{3\cdot3}{3+1}=\dfrac{9}{4}\)
25 tháng 7 2021
a, \(A=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)ĐK : \(x>0;x\ne1\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
b, \(A=\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{1}{3}\Rightarrow3\sqrt{x}-3=\sqrt{x}\Leftrightarrow2\sqrt{x}=3\)
\(\Leftrightarrow\sqrt{x}=\dfrac{3}{2}\Leftrightarrow x=\dfrac{9}{4}\)
c, \(P=\dfrac{\sqrt{x}-1}{\sqrt{x}}-9\sqrt{x}=\dfrac{\sqrt{x}-1-9x}{\sqrt{x}}\)
\(=1-\dfrac{1}{\sqrt{x}}-9\sqrt{x}\)Đặt \(\sqrt{x}=t^2\left(t>0\right)\)
\(1-t-9t^2=-\left(9t^2-t-1\right)=-\left(9t^2-2.3.\dfrac{1}{6}.t+\dfrac{1}{36}-\dfrac{37}{36}\right)\)
\(=-\left(3t-\dfrac{1}{6}\right)+\dfrac{37}{36}\le\dfrac{37}{36}\)
Dấu ''='' xảy ra khi t = 1/18 => t^2 = 1/324 => \(\sqrt{x}=\dfrac{1}{324}\Rightarrow x=\dfrac{1}{104876}\)
Vậy GTLN P là 37/36 khi x = 1/104876
