K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
Coi như bài toán đã cho là x;y;z hết từ điều kiện đến biểu thức (lẫn lộn abc với xyz)
Đặt \(\left(x^3;y^3;z^3\right)=\left(a^2;b^2;c^2\right)\Rightarrow abc=1\)
Ta có: \(Q=\dfrac{1}{a^2+b^2+b^2+1+2}+\dfrac{1}{b^2+c^2+c^2+1+2}+\dfrac{1}{c^2+a^2+a^2+1+2}\)
\(Q\le\dfrac{1}{2ab+2b+2}+\dfrac{1}{2bc+2c+2}+\dfrac{1}{2ca+2a+2}\)
\(Q\le\dfrac{1}{2}\left(\dfrac{1}{ab+b+1}+\dfrac{ab}{ab.bc+abc+ab}+\dfrac{b}{cab+ab+b}\right)\)
\(Q\le\dfrac{1}{2}\left(\dfrac{1}{ab+b+1}+\dfrac{ab}{b+1+ab}+\dfrac{b}{1+ab+b}\right)=\dfrac{1}{2}\)
1 tháng 9 2021
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(AB^2+AD^2=BD^2\)
\(\Leftrightarrow BD^2=6^2+8^2=100\)
hay BD=10(cm)
Ta có: ABCD là hình chữ nhật
mà O là giao điểm của hai đường chéo AC và BD
nên O là trung điểm chung của AC và BD
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAD vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(AH\cdot BD=AB\cdot AD\)
\(\Leftrightarrow AH=4.8\left(cm\right)\)
Ta có: ΔABD vuông tại A
mà AO là đường trung tuyến ứng với cạnh huyền BD
nên \(AO=\dfrac{BD}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAHO vuông tại H, ta được:
\(AO^2=AH^2+HO^2\)
\(\Leftrightarrow HO^2=5^2-4.8^2=1.96\)
hay HO=1,4(cm)
Diện tích tam giác AHO là:
\(S_{AHO}=\dfrac{HA\cdot HO}{2}=\dfrac{1.4\cdot4.8}{2}=3.36\left(cm^2\right)\)
9 tháng 9 2021
10: Ta có: \(\left(\dfrac{x-4}{x-2\sqrt{x}}+\dfrac{3}{\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}+2}{\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}-2}\right)\)
\(=\dfrac{x+3\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{x-4-x}\)
\(=\dfrac{-x-3\sqrt{x}+4}{4}\)
MD
0
LA
Giúp mình với ạ, mình cần gấp lắm ạ!
1
AH
Akai Haruma
Giáo viên
7 tháng 8 2021
Lời giải:
Đặt \(\sqrt[3]{5\sqrt{2}+7}=m; \sqrt[3]{5\sqrt{2}-7}=n\)
\(m^3-n^3=14\)
\(mn=1\)
\((a+b+c)^3=(m-n)^3=m^3-3mn(m-n)-n^3=14-3(m-n)\)
\(\Leftrightarrow (a+b+c)^3=14-3(a+b+c)\)
\(\Leftrightarrow (a+b+c)^3+3(a+b+c)-14=0\)
\(\Leftrightarrow (a+b+c)^2[(a+b+c)-2]+2(a+b+c)(a+b+c-2)+7(a+b+c-2)=0\)
\(\Leftrightarrow (a+b+c-2)[(a+b+c)^2+2(a+b+c)+7]=0\)
Dễ thấy biểu thức trong ngoặc vuông $>0$ nên $a+b+c-2=0$
$\Leftrightarrow a+b+c=2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-1}{2}=\frac{3}{2}$
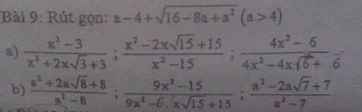
Bài 9:
Ta có: \(a-4+\sqrt{16-8a+a^2}\)
\(=a-4+\sqrt{\left(a-4\right)^2}\)
\(=a-4+a-4\)
=2a-8
a)\(\dfrac{x^2-3}{x^2+2x\sqrt{3}+3}=\dfrac{\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)}{\left(x+\sqrt{3}\right)^2}=\dfrac{x-\sqrt{3}}{x+\sqrt{3}}\)
\(\dfrac{x^2-2x\sqrt{15}+15}{x^2-15}=\dfrac{\left(x-\sqrt{15}\right)^2}{\left(x-\sqrt{15}\right)\left(x+\sqrt{15}\right)}=\dfrac{x-\sqrt{15}}{x+\sqrt{15}}\)
\(\dfrac{4x^2-6}{4x^2-4x\sqrt{6}+6}=\dfrac{\left(2x-\sqrt{6}\right)\left(2x+\sqrt{6}\right)}{\left(2x-\sqrt{6}\right)^2}=\dfrac{2x+\sqrt{6}}{2x-\sqrt{6}}\)
b) \(\dfrac{a^2+2a\sqrt{8}+8}{a^2-8}=\dfrac{\left(a+\sqrt{8}\right)^2}{\left(a+\sqrt{8}\right)\left(a-\sqrt{8}\right)}=\dfrac{a+\sqrt{8}}{a-\sqrt{8}}\)
\(\dfrac{9x^2-15}{9x^2-6x\sqrt{15}+15}=\dfrac{\left(3x-\sqrt{15}\right)\left(3x+\sqrt{15}\right)}{\left(3x-\sqrt{15}\right)^2}=\dfrac{3x+\sqrt{15}}{3x-\sqrt{15}}\)
\(\dfrac{a^2-2a\sqrt{7}+7}{a^2-7}=\dfrac{\left(a-\sqrt{7}\right)^2}{\left(a-\sqrt{7}\right)\left(a+\sqrt{7}\right)}=\dfrac{a-\sqrt{7}}{a+\sqrt{7}}\)