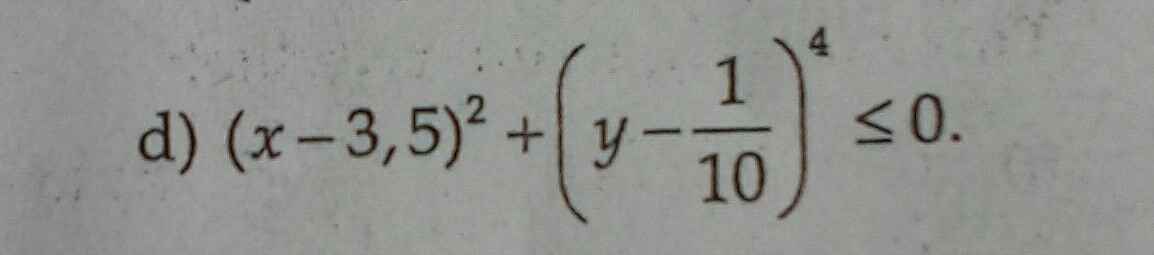Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(f\left(-2\right)=3.\left(-2\right)^2-1=3.4-1=11\\ f\left(\dfrac{1}{2}\right)=3.\left(\dfrac{1}{2}\right)^2-1=3.\left(\dfrac{1}{4}\right)-1=\dfrac{3}{4}-1=-\dfrac{1}{4}\\ f\left(\dfrac{-2}{\sqrt[]{3}}\right)=3.\left(\dfrac{-2}{\sqrt[]{3}}\right)^2-1=3.\left(\dfrac{4}{3}\right)-1=4-1=3\\ f\left(a+1\right)=3.\left(a+1\right)^2-1=3.\left(a^2+2a+1\right)-1=3a^2+6a+3-1=3a^2+6a+2\)

a: \(A=\left(-6x^3+6x^3\right)+\left(2x^2+5x^2\right)+\left(5x-2x\right)-1=7x^2+3x-1\)
b: Hệ số cao nhất là 7
Hệ số tự do là -1

a: \(f\left(x\right)+g\left(x\right)=x^3-3x^2+6x-8+x^3-6x^2+12x-8\)
\(=2x^3-9x^2+18x-16\)
b: \(f\left(1\right)=1^3-3\cdot1^2+6\cdot1-8=1-3+6-8=-2+6-8=4-8=-4\)
\(g\left(-1\right)=-6\cdot\left(-1\right)^2+\left(-1\right)^3-8+12\cdot\left(-1\right)\)
\(=-6\cdot1-1-8-12\)
=-6-21
=-27
c: f(x)-g(x)=0
=>f(x)=g(x)
\(\Leftrightarrow x^3-3x^2+6x-8=x^3-6x^2+12x-8\)
\(\Leftrightarrow3x^2-6x=0\)
=>3x(x-2)=0
=>x=0 hoặc x=2

Bài 7:
Đặt f(x)=a; g(x)=b
Theo đề, ta có: \(\left\{{}\begin{matrix}a+b=5x^2-2x+3\\a-b=x^2-2x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=6x^2-4x+8\\a-b=x^2-2x+5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=3x^2-2x+4\\g\left(x\right)=3x^2-2x+4-x^2+2x-5=2x^2-1\end{matrix}\right.\)

Gọi x,y,z là số học sinh khối 6, 7, 8
(x,y,z>0, đvị là học sinh)
Đã biết khối học sinh lớp 8 ít hơn số hs khối 6 là 120 hs
x-z=120
x, y, z tỉ lệ với 8, 7, 5
x/8=y/7=z/5
Áp dụng tính chất dãy tỉ số bằng nhau có:
x/8=y/7=z/5= x-z/8-5=120/3=40
=> x/8= 40 => x=40.8=320 => số hs khối 6 là 320 hs
y/7= 40 y=40.7= 280 số hs khối 7 là 280 hs
z/5= 40 z=40.5=200 số hs khối 8 là 200 hs

Ta có: \(\left(x-3.5\right)^2\ge0\forall x\)
\(\left(y-\dfrac{1}{10}\right)^4\ge0\forall y\)
Do đó: \(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(\dfrac{7}{2};\dfrac{1}{10}\right)\)
do
\(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4\ge0\)
mà ta có \(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4\le0\)
nên \(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4=0\)
suy ra \(\left\{{}\begin{matrix}x-3,5=0\\y-\dfrac{1}{10}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3,5\\y=\dfrac{1}{10}\end{matrix}\right.\)
tick mik nha

Bài 5:
a: \(=4x^2y^3\)
b: \(=\dfrac{9}{2}x^2y\)
c: \(=xyz^2\left(\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{1}{2}\right)=xyz^2\)
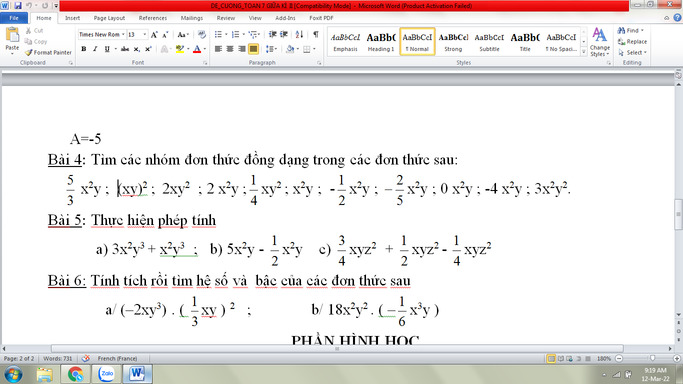
Bài 4
Nhóm 1: \(\dfrac{5}{3}x^2y,2x^2y,x^2y,\dfrac{1}{2}x^2y,\dfrac{-1}{2}x^2y,\dfrac{-2}{5}x^2y,0x^2y,-4x^2y\)
Nhóm 2: \(\left(xy\right)^2,3x^2y^2\)
Bài 5
\(a,3x^2y^3+x^2y^3\)
\(=4x^2y^3\)
\(b,5x^2y-\dfrac{1}{2}x^2y\)
\(=\left(5-\dfrac{1}{2}\right)\left(x^2y\right)\)
\(=\dfrac{9}{2}x^2y\)
\(c,\dfrac{3}{4}xyz^2+\dfrac{1}{2}xyz^2-\dfrac{1}{4}xyz^2\)
\(=\left(\dfrac{3}{4}+\dfrac{1}{2}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=\left(\dfrac{3}{4}+\dfrac{2}{4}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=xyz^2\)
Bài 6
\(a,\left(-2xy^3\right)\left(\dfrac{1}{3}xy\right)^2\)
\(=\left(-2.\dfrac{1}{9}\right)\left(x.x^2\right)\left(y^3y^2\right)\)
\(=\dfrac{-2}{9}x^3y^5\)
Bậc: 3 + 5 = 8
Hệ số: \(\dfrac{-2}{9}\)
\(b,18x^2y^2\left(\dfrac{-1}{6}x^3y\right)\)
\(=\left(-18.\dfrac{1}{6}a\right)\left(x^2x^2\right)\left(y^2y^3\right)\)
\(=-3ax^4y^5\)
Bậc: 4 + 5 = 9
Hệ số: \(-3a\)

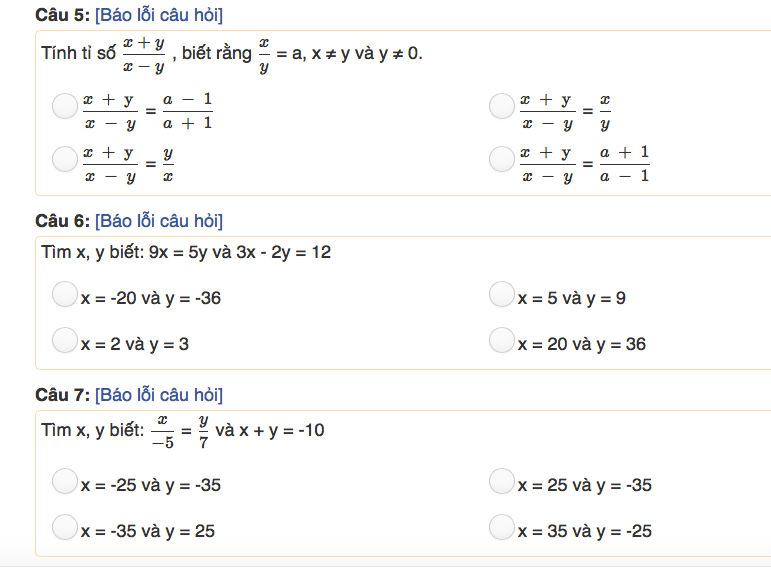
Câu 5:
\(\dfrac{x}{y}=a\Rightarrow\dfrac{x}{a}=\dfrac{y}{1}=\dfrac{x-y}{a-1}=\dfrac{x+y}{a+1}\)
\(\Rightarrow\dfrac{x+y}{x-y}=\dfrac{a+1}{a-1}\)
Câu 6:
\(9x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{3x}{15}=\dfrac{2y}{18}=\dfrac{3x-2y}{15-18}=\dfrac{12}{-3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).5=-20\\y=\left(-4\right).9=-36\end{matrix}\right.\)
Câu 7:
\(\dfrac{x}{-5}=\dfrac{y}{7}=\dfrac{x+y}{-5+7}=\dfrac{-10}{2}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).\left(-5\right)=25\\y=\left(-5\right).7=-35\end{matrix}\right.\)


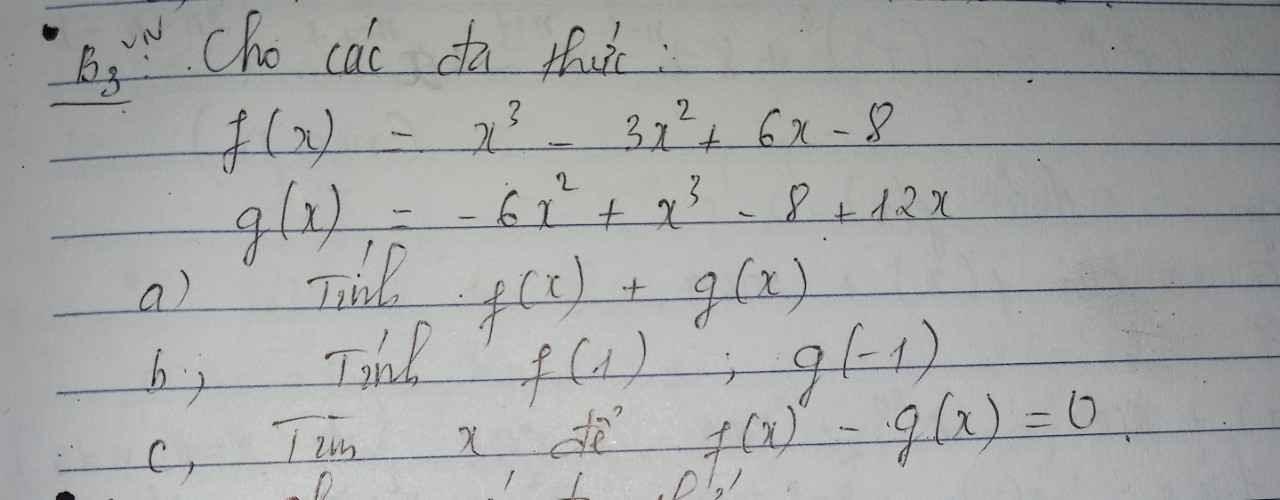
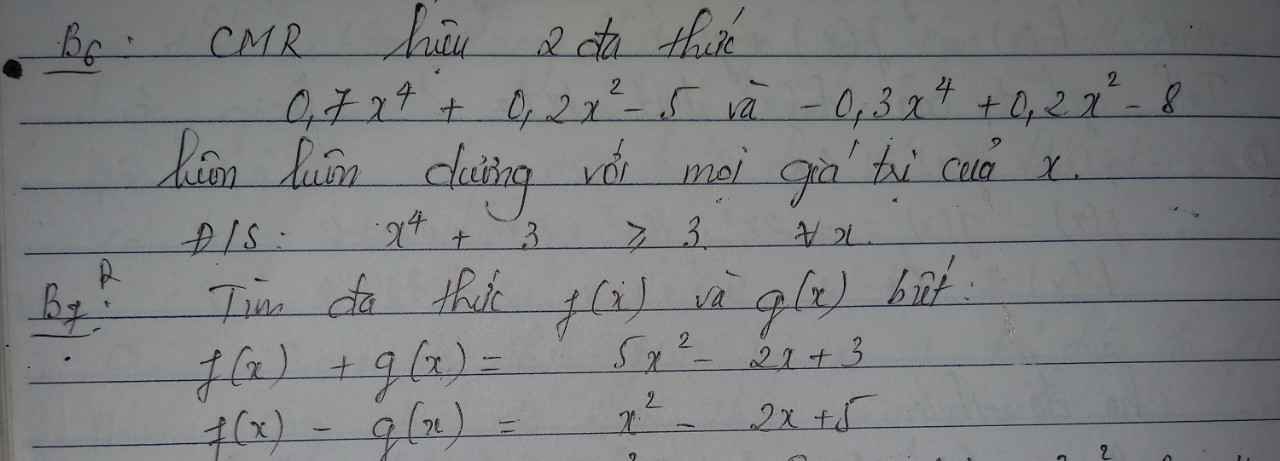
 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước