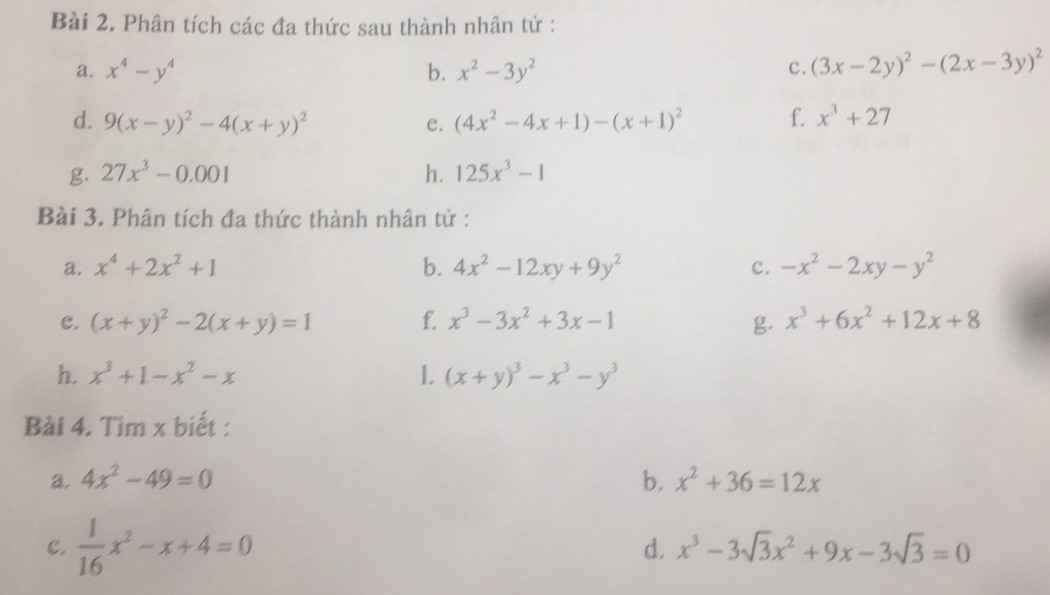K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DX
0
DX
0
NM
0
NM
0
NM
2
5 tháng 2 2021
- AD tính chất định lý talet vào tam giác EPF có MN // FP ta được :
\(\dfrac{EM}{EF}=\dfrac{EN}{EP}=\dfrac{MN}{FP}=\dfrac{12}{x+12}=\dfrac{10}{10+4}=\dfrac{y}{16}\)
\(\Rightarrow\dfrac{12}{x+12}=\dfrac{y}{16}=\dfrac{10}{14}=\dfrac{5}{7}\)
\(\Rightarrow\left\{{}\begin{matrix}y=\dfrac{80}{7}\\x=\dfrac{24}{5}\end{matrix}\right.\) ( cm )
Vậy ...
5 tháng 2 2021
Ta có: EP = EN + NP = 10 + 4 = 14 (cm)
Xét tam giác EFP có: MN // FP (gt)
=> \(\dfrac{MN}{FP}=\dfrac{EN}{EP}=\dfrac{EM}{EF}\) (hệ quả định lý Talét)
Thay số: \(\dfrac{y}{16}=\dfrac{10}{14}=\dfrac{12}{12+x}\)
=> \(\left\{{}\begin{matrix}y=\dfrac{80}{7}\\12+x=16,8< =>x=\dfrac{24}{5}\end{matrix}\right.\)
NM
1
5 tháng 2 2021
- AD tính chất định lý talet vào tam giác FPQ có MN // PQ ta được :
\(\dfrac{FM}{FQ}=\dfrac{FN}{FP}=\dfrac{MN}{PQ}=\dfrac{10}{y}=\dfrac{12}{16}=\dfrac{x}{20}\)
\(\Rightarrow\dfrac{10}{y}=\dfrac{x}{20}=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}y=\dfrac{40}{3}\\x=15\end{matrix}\right.\) ( cm )
Vậy ...
14 tháng 12 2022
a: BC=5cm
=>AM=2,5cm
b: Xet tứ giác AEMF có
góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét tứ giác AMBD có
E là trung điểm chung của AB và MD
MA=MB
Do đó: AMBD là hình thoi
27 tháng 8 2021
Bài 4:
d: Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)
e: Ta có: \(x^3-y^3-3x+3y\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-3\right)\)
DA
4
20 tháng 8 2021
2.
\(a,x^4-y^4=\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
\(b,x^2-3y^2=\left(x-y\sqrt{3}\right)\left(x+y\sqrt{3}\right)\)
\(c,\left(3x-2y\right)^2-\left(2x-3y\right)^2\\ =\left(3x-2y-2x+3y\right)\left(3x-2y+2x-3y\right)\\ =\left(x+y\right)\left(5x-5y\right)=5\left(x-y\right)\left(x+y\right)\)
\(d,9\left(x-y\right)^2-4\left(x+y\right)^2\\ =\left[3\left(x-y\right)-2\left(x+y\right)\right]\left[3\left(x-y\right)+2\left(x+y\right)\right]\\ =\left(3x-3y-2x-2y\right)\left(3x-3y+2x+2y\right)\\ =\left(x-5y\right)\left(5x-y\right)\)
\(e,\left(4x^2-4x+1\right)-\left(x+1\right)^2\\ =\left(2x-1\right)^2-\left(x+1\right)^2\\ =\left(2x-1-x-1\right)\left(2x-1+x+1\right)\\ =3x\left(x-2\right)\)
\(f,x^3+27=\left(x+3\right)\left(x^2+3x+9\right)\)
\(g,27x^3-0,001=\left(3x-0,1\right)\left(9x^2+0,027x+0,01\right)\)
\(h,125x^3-1=\left(5x-1\right)\left(25x^2+5x+1\right)\)
20 tháng 8 2021
Bài 3 :
a) \(x^4+2x^2+1=\left(x^2+1\right)^2\)
b) \(4x^2-12xy+9y^2=\left(2x-3y\right)^2\)
c) \(-x^2-2xy-y^2=-\left(x+y\right)^2\)
e) \(\left(x+y\right)^2-2\left(x+y\right)+1=\left(x+y-1\right)^2\)
f) \(x^3-3x^2+3x-1=\left(x-1\right)^3\)
g) \(x^3+6x^2+12x+8=\left(x+2\right)^3\)
h) \(x^3+1-x^2-x=\left(x+1\right)\left(x^2-x+1\right)-x\left(x+1\right)=\left(x+1\right)\left(x^2-2x+1\right)=\left(x+1\right)\left(x-1\right)^2\)
l) \(\left(x+y\right)^2-x^3-y^3=\left(x+y\right)^3-\left(x+y\right)\left(x^2-xy+y^2\right)=\left(x+y\right)\left(x^2+2xy+y^2-x^2+xy-y^2\right)=3xy\left(x+y\right)\)
