
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác ABD và tam giác ACDcó AB+BD>AD vàAC+CD>AD(BĐT tam giác ABD và ACD)
Cộng 2 vế lại với nhau ta được:
AB+AC+BD+CD>2AD
=>AB+AC+BC>2AD
Mà AB+AC+BC là chu vi của tam giác ABC
=>1/2(AB+AC+BC)>AD
Vậy nửa chu vi của tam giác ABC>AD

gọi (d) y=x
Thay x=1=>y=1=> (1;1)
Thay x=2=>y=2=> (2;2)
gọi (d1) y=-2x
Thay x=-1=> y=2=> (-1;2)
Thay x=1=>y=-2=> (1;-2)

Do \(\left|0,2x-3,1\right|\ge0\); \(\left|0,2x+3,1\right|\ge0\)
=> \(\left|0,2x-3,1\right|+\left|0,2x+3,1\right|\ge0\)
Mà theo đề bài: |0,2x - 3,1| + |0,2x + 3,1| = 0
=> \(\begin{cases}\left|0,2x-3,1\right|=0\\\left|0,2x+3,1\right|=0\end{cases}\)=> \(\begin{cases}0,2x-3,1=0\\0,2x+3,1=0\end{cases}\)=> \(\begin{cases}0,2x=3,1\\0,2x-3,1\end{cases}\), vô lý
Vì 0,2x = 0,2x; \(3,1\ne-3,1\)
Vậy không tồn tại giá trị của x thỏa mãn đề bài


Bài 1:
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI

Bài 2:
a: Xét ΔAMN và ΔAMP có
AM chung
MN=MP
AN=AP
Do đó: ΔAMN=ΔAMP


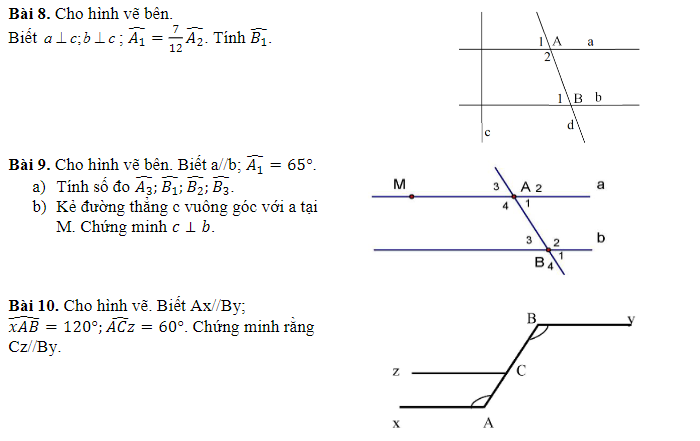
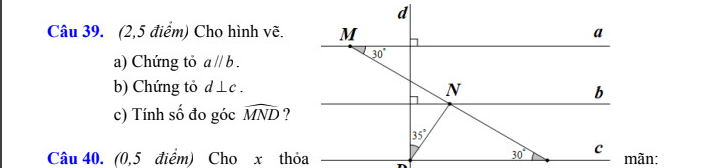
a, Vì a⊥d và b⊥d nên a//b
b, Gọi giao của MN và C là A
Ta có \(\widehat{DAM}=\widehat{AMa}=30^0\) mà 2 góc này ở vị trí SLT nên a//c
Mà a⊥d nên c⊥d
c, \(\widehat{MND}=30^0+\left(90^0-35^0\right)=85^0\)


bạn hỏi thế thì hỏi cả bài luôn à
đúng đấy!