
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có sinB=\(\dfrac{AH}{AB}\)\(\Rightarrow\)AH=AB.sinB=3,6.sin62=3,18
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{3,6^2-3,18^2}\)=1,69
\(_{\widehat{C}}\)=90-\(\widehat{B}\)=90-62=28\(^0\)
sinC=\(\dfrac{AB}{BC}\)\(\Rightarrow\)BC=\(\dfrac{AB}{sinC}\)=\(\dfrac{3,6}{sin28}\)=7,67
mà:CH=BC-BH=7,67-1,69=5,98
AC=\(\sqrt{BC^2-AB^2}\)(pytago)=\(\sqrt{7,67^2-3,6^2}\)=6.77

a: \(A=\sqrt{x^2+2x+5}=\sqrt{x^2+2x+1+4}\)
=>\(A=\sqrt{\left(x+1\right)^2+4}>=\sqrt{4}=2\)
b: \(B=\sqrt{x^2-4x+4+1}=\sqrt{\left(x-2\right)^2+1}>=1\)

\(P=\dfrac{2\sqrt{x}+1+\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+1+1-x}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{-x+2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}=\dfrac{-x+2\sqrt{x}+2}{x+3\sqrt{x}+2}\)

Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$

\(a,=2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}\\ =2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{5}-1}\\ =2\left(\sqrt{5}-1\right)\sqrt{6-2\sqrt{5}}\\ =2\left(\sqrt{5}-1\right)\sqrt{\left(\sqrt{5}-1\right)^2}\\ =2\left(\sqrt{5}-1\right)^2=2\left(6-2\sqrt{5}\right)=12-4\sqrt{5}\\ b,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)

a.
Ta có: \(\sqrt{x^2+12}>\sqrt{x^2+5}\Rightarrow\sqrt{x^2+12}-\sqrt{x^2+5}>0\)
\(\Rightarrow3x-5=\sqrt{x^2+12}-\sqrt{x^2+5}>0\Rightarrow x>\dfrac{5}{3}\)
Do đó:
\(\sqrt{x^2+12}+5=3x+\sqrt{x^2+5}\)
\(\Leftrightarrow3\left(x-2\right)+\sqrt{x^2+5}-3-\left(\sqrt{x^2+12}-4\right)=0\)
\(\Leftrightarrow3\left(x-2\right)+\dfrac{x^2-4}{\sqrt{x^2+5}+3}-\dfrac{x^2-4}{\sqrt{x^2+12}+4}=0\)
\(\Leftrightarrow\left(x-2\right)\left(3+\dfrac{x+2}{\sqrt{x^2+5}+3}-\dfrac{x+2}{\sqrt{x^2+12}+4}\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[3+\left(x+2\right)\left(\dfrac{1}{\sqrt{x^2+5}+3}-\dfrac{1}{\sqrt{x^2+12}+4}\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(3+\dfrac{\left(x+2\right)\left(\sqrt{x^2+12}-\sqrt{x^2+5}+1\right)}{\left(\sqrt{x^2+5}+3\right)\left(\sqrt{x^2+12}+4\right)}\right)=0\)
\(\Leftrightarrow x-2=0\) (do \(x>\dfrac{5}{3}\) nên ngoặc phía sau luôn dương)
\(\Leftrightarrow x=2\)
b.
\(\Delta=\left(m-1\right)^2-4\left(-m^2+m-2\right)=5m^2-6m+9=5\left(m-\dfrac{3}{5}\right)^2+\dfrac{36}{5}>0\)
Phương trình đã cho luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-m^2+m-2\end{matrix}\right.\)
\(Q=\left(\dfrac{x_1}{x_2}\right)^2+\left(\dfrac{x_2}{x_1}\right)^2+2-2=\left(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}\right)^2-2\)
\(=\left(\dfrac{x_1^2+x_2^2}{x_1x_2}\right)^2-2=\left[\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}\right]^2-2\)
\(=\left[\dfrac{\left(m-1\right)^2-2\left(-m^2+m-2\right)}{-m^2+m-2}\right]^2-2=\left(\dfrac{3m^2-4m+5}{m^2-m+2}\right)^2-2\)
Ta có: \(\dfrac{3m^2-4m+5}{m^2-m+2}=\dfrac{3\left(m-\dfrac{2}{3}\right)^2+\dfrac{11}{3}}{\left(m-\dfrac{1}{2}\right)^2+\dfrac{7}{4}}>0\)
\(\dfrac{3m^2-4m+5}{m^2-m+2}=\dfrac{21m^2-28m+35}{7\left(m^2-m+2\right)}=\dfrac{22\left(m^2-m+2\right)-\left(m^2+6m+9\right)}{7\left(m^2-m+2\right)}=\dfrac{22}{7}-\dfrac{\left(m+3\right)^2}{7\left(m^2-m+2\right)}\le\dfrac{22}{7}\)
\(\Rightarrow0< \dfrac{3m^2-4m+5}{m^2-m+2}\le\dfrac{22}{7}\)
\(\Rightarrow Q\le\left(\dfrac{22}{7}\right)^2-2\)
Dấu "=" xảy ra khi \(m+3=0\Leftrightarrow m=-3\)



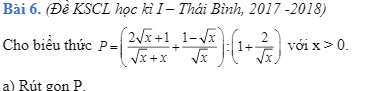
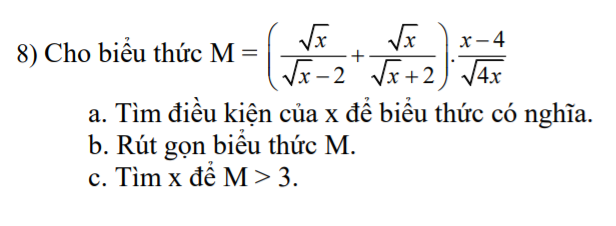





Bài 1:
a) \(=\dfrac{\sqrt{5}.\sqrt{7}}{5}=\dfrac{\sqrt{35}}{5}\)
b) \(=\dfrac{\left|y\right|}{\sqrt{3}}=\dfrac{\sqrt{3}y}{3}\)
c) \(=\dfrac{\sqrt{2}}{\sqrt{t}}=\dfrac{\sqrt{2t}}{t}\)
d) \(=\sqrt{\dfrac{7p^2-3p^2}{7}}=\sqrt{\dfrac{4p^2}{7}}=\dfrac{2\left|p\right|}{\sqrt{7}}=\dfrac{-2\sqrt{7}p}{7}\)
Bài 2:
a) \(=\dfrac{\sqrt{21}-\sqrt{15}}{3}\)
b) \(=\dfrac{10\left(4+3\sqrt{2}\right)}{16-18}=-20-15\sqrt{2}\)
c) \(=\dfrac{\left(3\sqrt{10}-5\right)\left(6+\sqrt{10}\right)}{36-10}=\dfrac{18\sqrt{10}+30-30-5\sqrt{10}}{26}=\dfrac{13\sqrt{10}}{26}=\dfrac{\sqrt{10}}{2}\)
Còn câu d bài 2 thì sao ạ??