
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


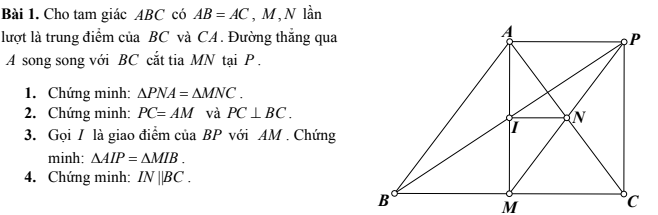
4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC

1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔBAC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC

1. Tam giác AOC và tam giác BOD có: AO = BO; CO = DO: góc AOC = góc BOD (đối đỉnh)
--> tam giác AOC = tam giác BOD (c.g.c)
--> góc ACO = góc ODB
Mà 2 góc này ở vị trí so le trong
--> AC // BD

Bài 4:
a: Xét ΔBDC vuông tại D có \(BC^2=BD^2+DC^2\)
nên BC=10(cm)
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{EAC}\) chung
Do đó: ΔABD=ΔACE
c: Ta có: ΔABD=ΔACE
nên AD=AE
hay ΔADE cân tại A
Xét ΔABC có
AE/AB=AD/AC
nên DE//BC
d: Xét ΔDBC vuông tại D và ΔDKC vuông tại D có
DB=DK
DC chung
Do đó: ΔDBC=ΔDKC
Suy ra: \(\widehat{DBC}=\widehat{DKC}\left(1\right)\)
Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
EC=DB
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{ECB}=\widehat{DBC}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{ECB}=\widehat{DKC}\)


1/
Xét tg ABC có AB=AC => tg ABC cân tại A \(\Rightarrow\widehat{B}=\widehat{C}\) (Trong tg cân hai góc ở đáy = nhau)
BH=CH => AH là đường trung tuyến \(\Rightarrow AH\perp BC\) (trong tg cân đường trung tuyến xp từ đỉnh đồng thời là đường cao và đường trung trực)
2/ Ta có
\(MN\perp BC;CP\perp BC\) => MN//CP
MN=CP
=> Tứ giác MNPC là hình bình hành (Tứ giác có cặp cạnh đối // và = nhau thì tứ giác đó là hbh)
=> MN=CP; MC=NP; MP chung \(\Rightarrow\Delta MCP=\Delta PMN\left(c.c.c\right)\)
3/
Trong hình bình hành MNPC thì MP và NC là hai đường chéo hbh
=> I là trung điểm của NC (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)







a: \(A=2x^3-3x^2+4x+5\)
\(\dfrac{A}{B}=\dfrac{2x^3-3x^2+4x+5}{2x+1}\)
\(=\dfrac{2x^3+x^2-4x^2-2x+6x+3+2}{2x+1}=x^2-2x+3+\dfrac{2}{2x+1}\)
b: \(\dfrac{A\left(x\right)}{B\left(x\right)}=\dfrac{2x^3-3x^2+4x+a}{2x+1}\)
\(=\dfrac{2x^3+x^2-4x^2-2x+6x+3+a-3}{2x+1}\)
\(=x^2-2x+3+\dfrac{a-3}{2x+1}\)
Để A chia hết cho B thì a-3=0
=>a=3