K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SC
12 tháng 1 2022
Tuyệt vời, đợi mình load rồi mình hỏi thêm vào câu nữa nha bẹn
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 8 2021
1.
a.
ĐKXĐ: \(x^2-1>0\Rightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)
\(log_2\left(x^2-1\right)=3\)
\(\Rightarrow x^2-1=8\)
\(\Leftrightarrow x^2=9\)
\(\Rightarrow x=\pm3\) (tm)
b.
ĐKXĐ: \(x>0\)
\(log_3x+log_{\sqrt{3}}x+log_{\dfrac{1}{3}}x=6\)
\(\Leftrightarrow log_3x+2log_3x-log_3x=6\)
\(\Leftrightarrow log_3x=3\)
\(\Rightarrow x=3^3=27\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 8 2021
c. ĐKXĐ: \(x>0\)
\(log_{\sqrt{2}}^2x+3log_2x+log_{\dfrac{1}{2}}x=2\)
\(\Leftrightarrow\left(2log_2x\right)^2+3log_2x-log_2x=2\)
\(\Leftrightarrow4log_2^2x+2log_2x-2=0\)
\(\Rightarrow\left[{}\begin{matrix}log_2x=-1\\log_2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\sqrt{2}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2021
Đặt \(f\left(x\right)=\dfrac{1}{3}x^3-x^2+mx+1\Rightarrow f'\left(x\right)=x^2-2x+m\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}x^2-2x+m\ge0;\forall x\ge1\\f\left(1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m+\dfrac{1}{3}\ge0\end{matrix}\right.\) \(\Rightarrow m\ge1\)
\(\Rightarrow m=\left\{1;2;3\right\}\)
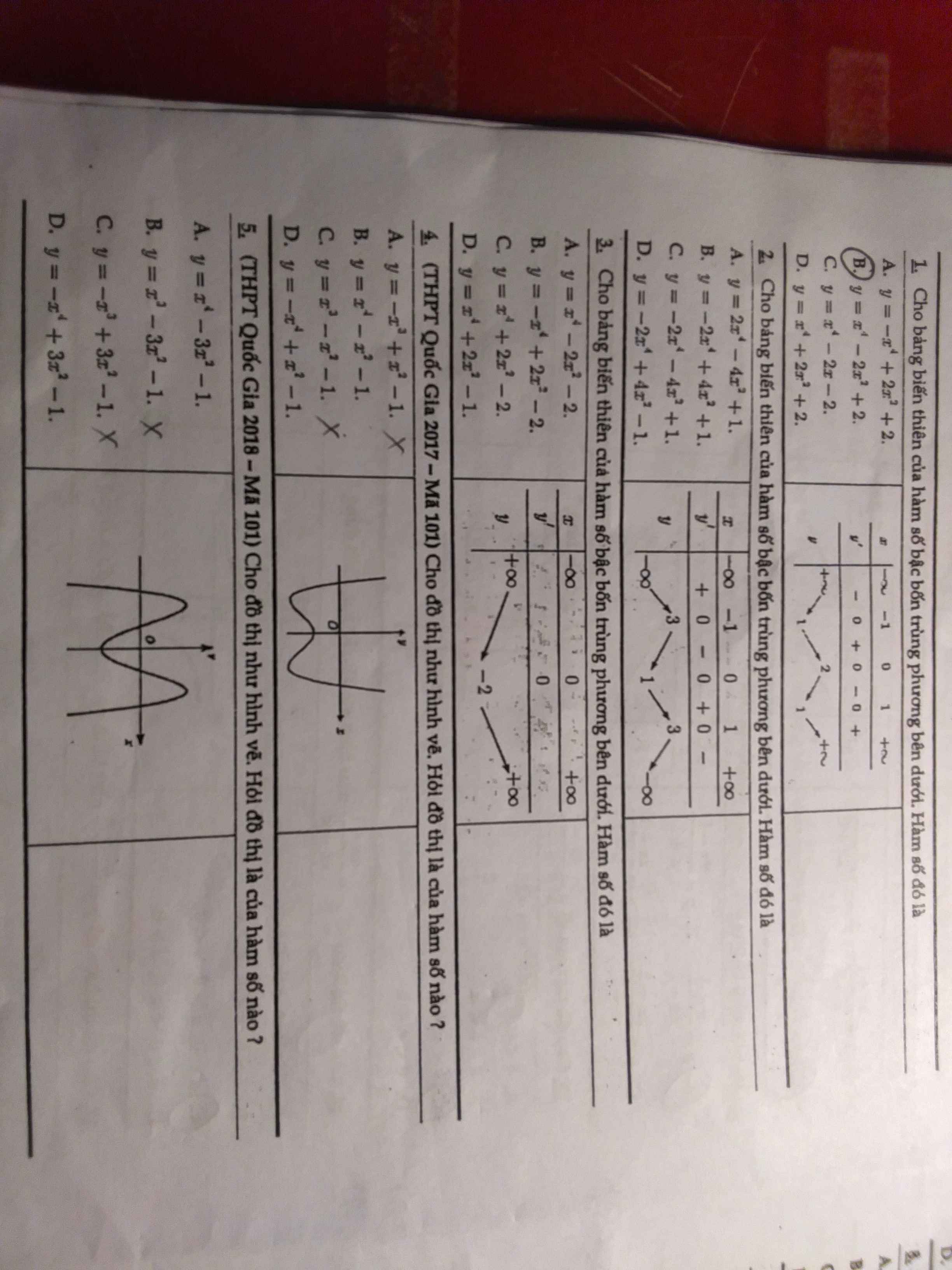
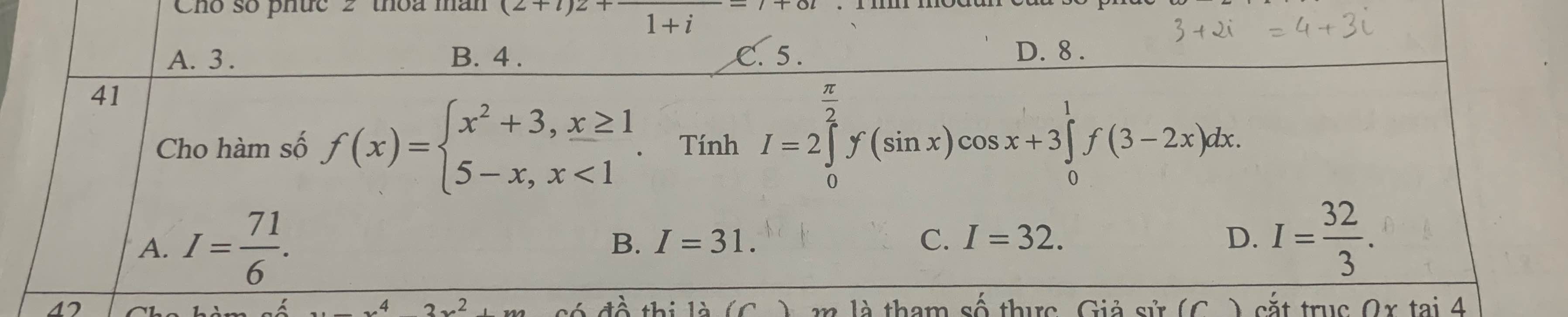
1. Chọn B.
2. Chọn B.
3. Chọn D.
4. Chọn B.
5. Chọn D.
6. Chọn A.
7. Chọn D.
8. Chọn A.
9. Chọn D.
10. Chọn C.
11. Chọn A.
12.Chọn B.