K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
0
AH
Akai Haruma
Giáo viên
22 tháng 12 2022
Lời giải:
a.
\(A=\frac{\sqrt{x}+6-(\sqrt{x}-6)}{(\sqrt{x}+6)(\sqrt{x}-6)}=\frac{12}{x-36}\)
b.
Để $A=2\Leftrightarrow \frac{12}{x-36}=2$
$\Leftrightarrow x-36=6\Leftrightarrow x=42$ (thỏa mãn)
DT
0
18 tháng 9 2021
\(4,\\ 2.B=\sqrt{x}-1+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\left(x>0\right)\\ B=\dfrac{x-\sqrt{x}+2-2\sqrt{x}}{\sqrt{x}}=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\)
\(3.x=\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}=\left(3+\sqrt{2}\right)+\left(3-\sqrt{2}\right)=6\)
Thay vào B, ta được \(B=\dfrac{6-3\sqrt{6}+2}{\sqrt{6}}=\dfrac{6\sqrt{6}-18+2\sqrt{6}}{6}=\dfrac{4\sqrt{6}-9}{3}\)
\(4.B=0\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}=0\Leftrightarrow x-3\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
\(7.B\in Z\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}-3+\dfrac{2}{\sqrt{x}}\in Z\\ \Leftrightarrow\dfrac{2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow x\in\left\{1;4\right\}\left(\sqrt{x}>0\right)\)
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$
1 tháng 11 2021
b: \(BC\cdot\sin B\cdot\sin C\)
\(=BC\cdot\dfrac{AC}{BC}\cdot\dfrac{AB}{BC}\)
\(=\dfrac{BC\cdot AH\cdot BC}{BC^2}=AH\)
D
15 tháng 12 2022
B3
1) \(\sqrt{ }\)(2x-1)2 =5
\(\Leftrightarrow\) |2x-1| =5
\(\Leftrightarrow\) 2x-1 =5 hoặc 2x -1 = -5
\(\Leftrightarrow\) 2x=6 hoặc 2x= -4
\(\Leftrightarrow\) x=3 hoặc x= -2
2) 4-5x = 144
\(\Leftrightarrow\) -5x =140
\(\Leftrightarrow\) x= -60
3) \(\sqrt{ }\)(2x-2)2=2x-2
\(\Leftrightarrow\) | 2x -2 | =2x-2
\(\Leftrightarrow\) 2x-2 =2x-2 hoặc 2x-2 =-2x +2
\(\Leftrightarrow\) 0x=0 (loại ) hoặc x=2 ( nhận )
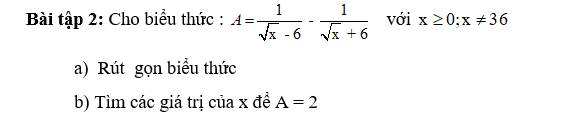
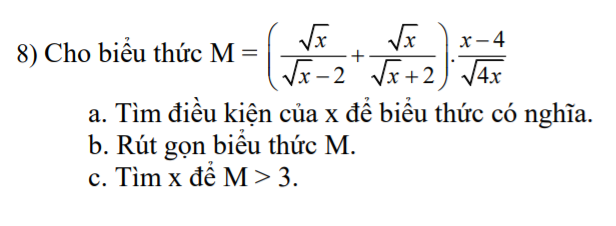
a: AC=12(cm)
\(\sin\widehat{C}=\dfrac{9}{15}=\dfrac{3}{5}\)
\(\Leftrightarrow C=37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)