
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3x . 2 + 15 = 33
3x . 2 = 33 - 15 = 18
3x = 18 : 2 = 9 = 32
=> x = 2


Ta có: \(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+...+\dfrac{1}{99\cdot100}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=\dfrac{1}{2}-\dfrac{1}{100}=\dfrac{50}{100}-\dfrac{1}{100}=\dfrac{49}{100}\)
\(A=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{99.100}\)
\(A=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A=\dfrac{1}{2}-\left(\dfrac{1}{3}-\dfrac{1}{3}\right)-\left(\dfrac{1}{4}-\dfrac{1}{4}\right)-\left(\dfrac{1}{5}-\dfrac{1}{5}\right)-...-\left(\dfrac{1}{99}-\dfrac{1}{99}\right)-\dfrac{1}{100}\)
\(A=\dfrac{1}{2}-0-0-0-...-0-\dfrac{1}{100}\)
\(A=\dfrac{1}{2}-\dfrac{1}{100}\)
\(A=\dfrac{50}{100}-\dfrac{1}{100}\)
\(A=\dfrac{49}{100}\)

\(a,\Rightarrow20\cdot2^x=160+1-1\\ \Rightarrow2^x=160:20=8=2^3\\ \Rightarrow x=3\\ b,\Rightarrow\left(4-x:2\right)^3=2\left(8-5\right)+1+1\\ \Rightarrow\left(4-x:2\right)^3=6+2=8=2^3\\ \Rightarrow4-x:2=2\\ \Rightarrow x:2=2\Rightarrow x=4\\ c,n\left(n+2017\right)\)
Với n chẵn thì \(n=2k\left(k\in N\right)\Rightarrow n\left(n+2017\right)=2k\left(n+2017\right)⋮2\)
Với n lẻ thì \(n=2k+1\left(k\in N\right)\Rightarrow n\left(n+2017\right)=n\left(2k+2018\right)=2n\left(k+1009\right)⋮2\)
Vậy \(n\left(n+2017\right)\) luôn chẵn
\(d,3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}=\left(2^3\right)^{100}=2^{300}\)

2S = 2 + 2^2 + 2^3 + ...+ 2^64
2S + 1 = 1 + 2 + 2^2 + ... + 2^64
2S - S = 2^64 - 1
Vậy S = 2^64 - 1
\(A=2^2+2^3+...+2^{62}+2^{63}\)
\(2A=2^3+2^4+...+2^{63}+2^{64}\)
\(2A-A=\left(2^3+2^4+...+2^{63}+2^{64}\right)-\left(2^2+2^3+...+2^{62}+2^{63}\right)\)
\(A=2^{64}-2^2\)

Bài 48:
1/ 17(-84) + 17(-16) = 17 \(\left[\left(-84\right)+\left(-16\right)\right]\) = 17. (-100) = -1700
2/ 15.58 - 15.48 = 15.(58 - 48) = 15 . 10 = 150
3/ -37.86 + 37.76 = 37 .(-86 + 76) = 37. (-10) = -370
4/ 1975 .(-115) + 1975.15 = 1975. (-115 + 15) = 1975 . (-100) = -197500
5/ 79.89 - 79.(-11) = 79. (89 + 11) = 79 . 100 = 7900
6/ 48.195 - 48 . 95 = 48. (195 - 95) = 48 . 100 = 4800
7/ 157.17 - 157.7 = 157. (17 - 7) = 157 . 10 = 1570
8/ 15(-176) + 15.76 = 15. (-176 + 6) = 15 . 100 = 1500
9/ 47.(-147) - 47 .(-47)= 47 (-147 + 47) = 47. (-100) = -4700
10/ 153.177 - 153.77 = 153. (177 - 77) = 153. 100 = 15300
11/ 15. (4 - 7) - 15. (5 - 3)
= 15. (-3) - 15. 2
= 15. (-3 - 2)
= 15. (-5)
= -75
12/ 73. (8 - 59) - 59. (8 - 73)
= 73. 8 - 73. 59 - 59. 8 + 73. 59
= 8. (73 - 59) + 73. (59 - 59)
= 8. (73 - 59) + 0
= 8. 14
= 112
13/ 159. (18 - 59) - 59. (18 - 159)
= 159. 18 - 159. 59 - 59. 18 + 59. 159
= 18.(159 - 59) - 59. (159 - 159)
= 18.(159 - 59) - 0
= 18. 100
= 1800
14/ -145. (13 - 57) + 57. (10 - 145)
= -145. 13 + 145. 57 + 57. 10 - 57. 145
= -145. 13 + 57. 10
= -1885 + 570
= 2455
Những câu còn lại tương tự


Bài 3:
\(A=\dfrac{10^9+1}{10^{10}+1}\Rightarrow10A=\dfrac{10^{10}+10}{10^{10}+1}\Rightarrow10A-1=\dfrac{9}{10^{10}+1}\)
\(B=\dfrac{10^8+1}{10^9+1}\Rightarrow10B=\dfrac{10^9+10}{10^9+1}\Rightarrow10B-1=\dfrac{9}{10^9+1}\)
\(Do\) \(\dfrac{9}{10^{10}+1}< \dfrac{9}{10^9+1}\Rightarrow10A-1< 10B-1\Rightarrow10A< 10B\Rightarrow A< B\)

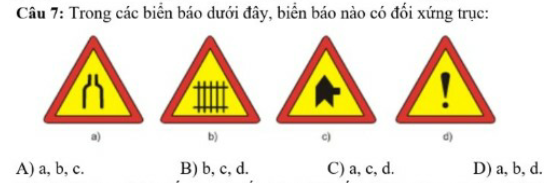

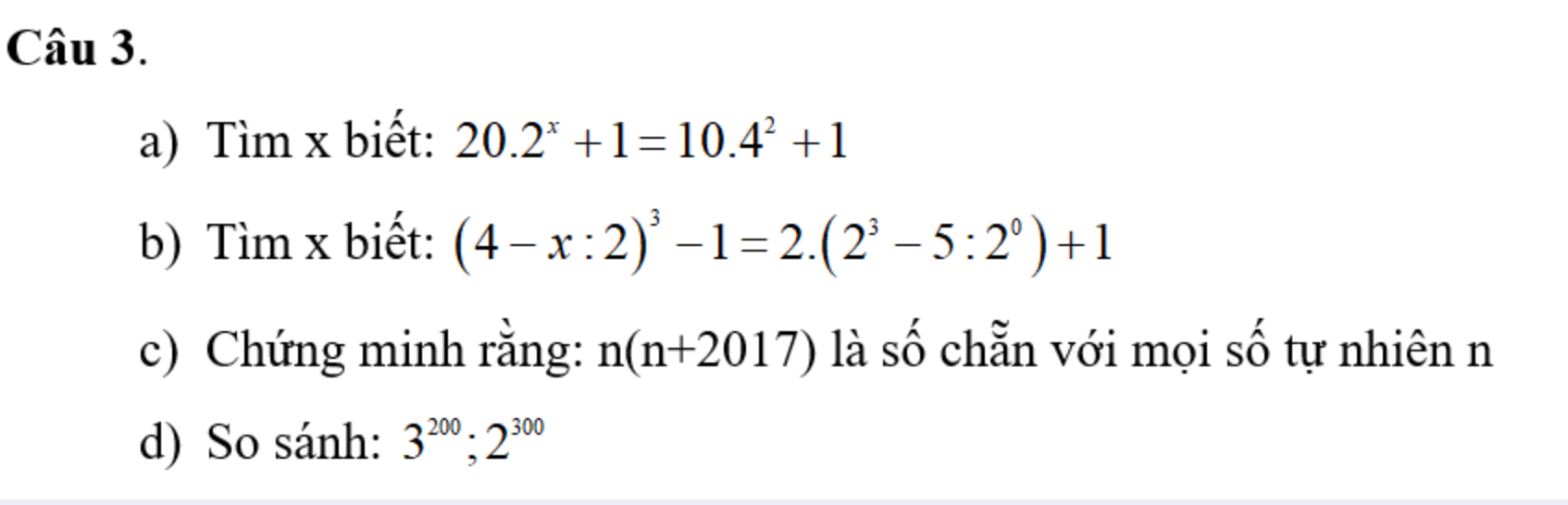 giúp mình với, mình cần gấp lắm, 5p phải nộp rồi
giúp mình với, mình cần gấp lắm, 5p phải nộp rồi
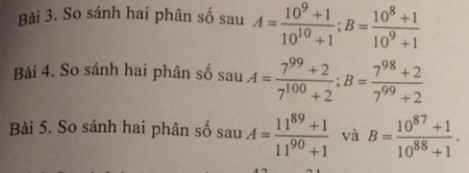
\(A=7\left(1+7+7^2\right)+...+7^{118}\left(1+7+7^2\right)\)
\(=57\left(1+...+7^{118}\right)⋮57\)