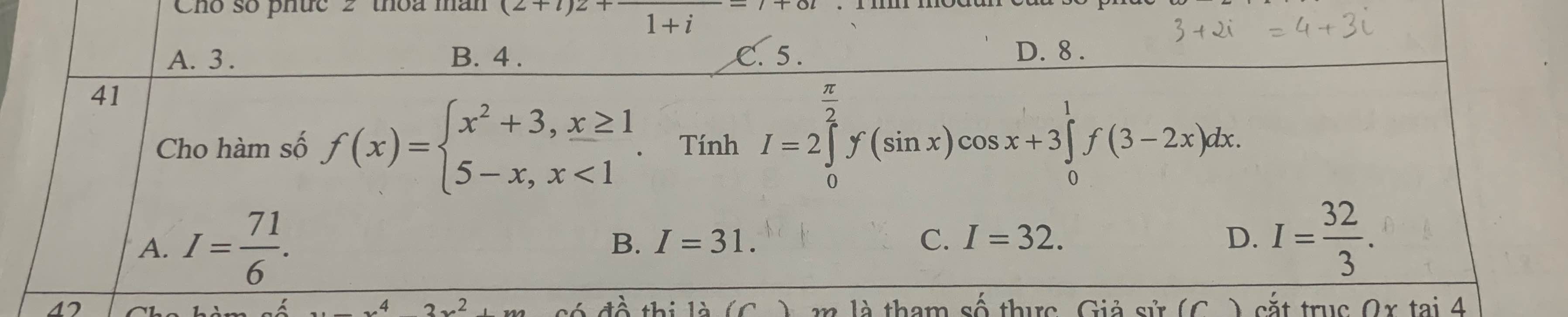K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
13 tháng 10 2021
Lời giải:
$y'=x^2+2mx+(m^2-4)=0$
Để hàm số đạt cực đại tại $x=1$ thì trước tiên, $y'=0$ tại $x=1$
$\Leftrightarrow 1+2m+m^2-4=0$
$\Leftrightarrow m^2+2m-3=0$
$\Leftrightarrow m=1$ hoặc $m=-3$
$f''(x)=2x+2m$.
Với $m=1$ thì $f''(1)=4>0$, trong khi đó với $m=-3$ thì $f''(1)=-4<0$
Do đó hàm đạt cực đại tại $x=1$ khi $m=-3$
Đáp án D
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 6 2021
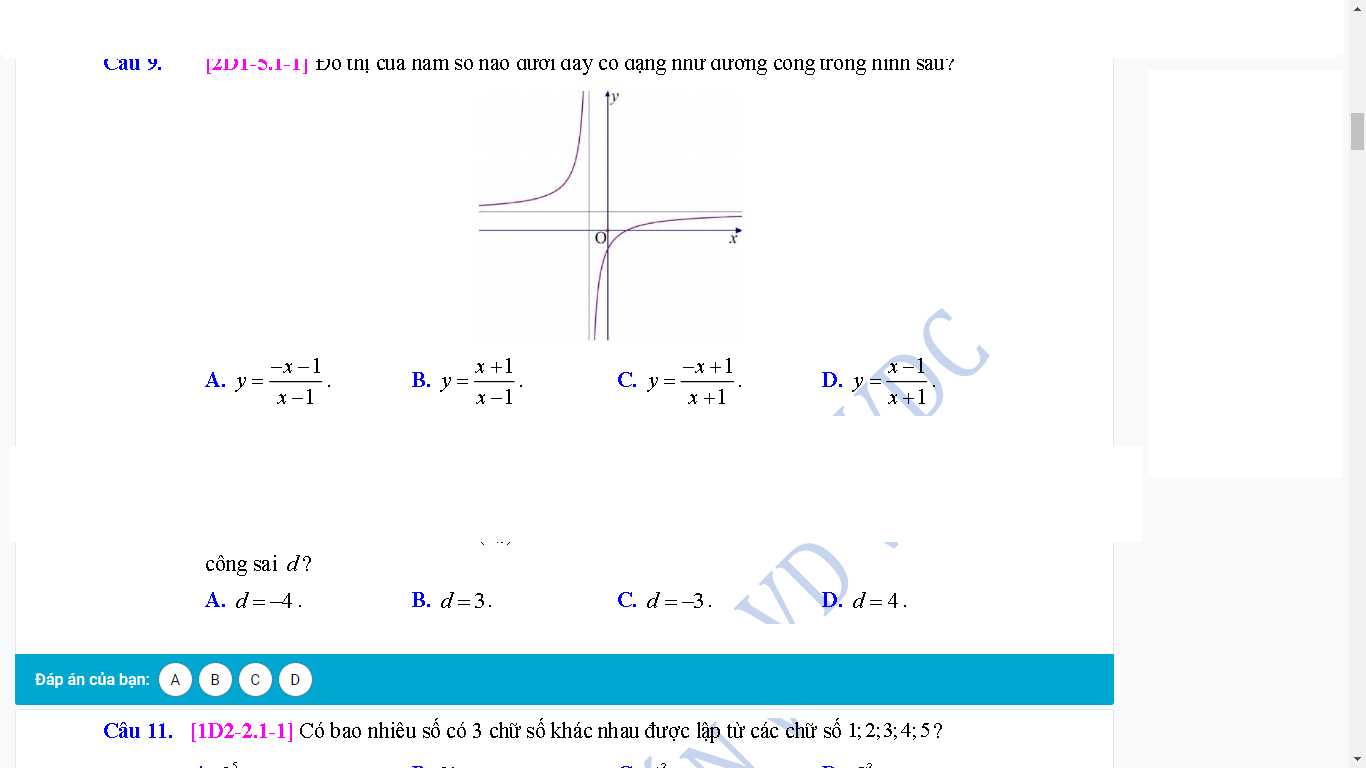
- Tiệm cận đứng của đồ thị là 1 giá trị âm nên loại A và B
- Hàm đồng biến trên các khoảng xác định nên loại C
Vậy D là đáp án đúng
NT
0
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
6 tháng 5 2021
Câu 35 Diện tích tam giác ABC là \(\dfrac{1}{2}\).AB.AC=\(\dfrac{1}{2}\).a\(^2\)
thể tích lăng trụ ABC.A'B'C'=a\(\sqrt{3}\).\(\dfrac{1}{2}\)a\(^2\)=a\(^3\)\(\dfrac{\sqrt{3}}{2}\)
Câu 36 Gọi O là giao điểm của AC và DB
AC=\(\sqrt{2}\)a => AO=\(\dfrac{\sqrt{2}}{2}\)a
Mà góc SAC=45 => SO=AO=\(\dfrac{\sqrt{2}}{2}\)a
thể tích khối chóp S.ABCD = \(\dfrac{1}{3}\).\(\dfrac{\sqrt{2}}{2}\)a.a\(^2\)=\(\dfrac{\sqrt{2}}{6}\)a\(^3\)
Câu 37 \(\dfrac{Vs.A'B'C'}{Vs.ABC}\)=\(\dfrac{SA'}{SA}\).\(\dfrac{SB'}{SB}\).\(\dfrac{SC'}{SC}\)=\(\dfrac{1}{8}\)
tương tự \(\dfrac{Vs.D'B'C'}{Vs.DBC}\)=\(\dfrac{1}{8}\)=> \(\dfrac{Vs.A'B'C'D'}{Vs.ABCD}\)=\(\dfrac{1}{8}\)
