
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`1)\sqrt{50}-3\sqrt{8}+\sqrt{32}=5\sqrt{2}-6\sqrt{2}+4\sqrt{2}=3\sqrt{2}`
`2)`
`a)\sqrt{x^2-4x+4}=1`
`<=>\sqrt(x-2)^2}=1`
`<=>|x-2|=1`
`<=>[(x-2=1),(x-2=-1):}<=>[(x=3),(x=1):}`
`b)\sqrt{x^2-3x}-\sqrt{x-3}=0` `ĐK: x >= 3`
`<=>\sqrt{x}\sqrt{x-3}-\sqrt{x-3}=0`
`<=>\sqrt{x-3}(\sqrt{x}-1)=0`
`<=>[(\sqrt{x-3}=0),(\sqrt{x}-1=0):}`
`<=>[(x-3=0),(\sqrt{x}=1):}<=>[(x=3(t//m)),(x=1(ko t//m)):}`

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1x_2=-\dfrac{7}{2}\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\dfrac{37}{4}\)
\(B=x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\dfrac{153}{8}\)
\(C=x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2\left(x_1x_2\right)^2=\dfrac{977}{16}\)
\(D=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\dfrac{\sqrt{65}}{2}\)
\(E=\left(2x_1+x_2\right)\left(2x_2+x_1\right)=2\left(x_1^2+x_2^2\right)+5x_1x_2=1\)

`a,` Đthang đi qua `A(3, 12)`.
`-> x = 3, y = 12 in y`.
`<=> 12 = 9a.`
`<=> a = 12/9 = 4/3.`
`b,` Đthang đi qua `B(-2;3)`.
`=> x = -2, y = 3 in y`.
`<=> 3=4a`.
`<=> a = 3/4`.

`3x^2+10x+3=0`
Ptr có: `\Delta'=5^2-3.3=16 > 0`
`=>` Ptr có `2` nghiệm pb
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=-10/3),(x_1 .x_2=c/a=1):}`
~~~~~~~~~~~~~
`A=x_1 ^2+x_2 ^2`
`A=(x_1+x_2)^2-2x_1 .x_2`
`A=(-10/3)^2-2.1=82/9`
_______________________________________________________
`B=x_1 ^3+x_2 ^3`
`B=(x_1+x_2)(x_1 ^2-x_1 .x_2+x_2 ^2)`
`B=(x_1+x_2)[(x_1+x_2)^2 -3x_1 .x_2]`
`B=(-10/3).[(-10/3)^2-3.1]=-730/27`
_______________________________________________________
`C=x_1 ^4+x_2 ^4`
`C=(x_1 ^2+x_2 ^2)^2 -2x_1 ^2 .x_2 ^2`
`C=[(x_1+x_2)^2-2x_1 .x_2]^2-2(x_1 .x_2)^2`
`C=[(-10/3)^2-2.1]^2-2. 1^2=6562/81`
_______________________________________________________
`D=|x_1-x_2|`
`D=\sqrt{(x_1-x_2)^2}`
`D=\sqrt{(x_1+x_2)^2-4x_1.x_2}`
`D=\sqrt{(-10/3)^2-4.1}=8/3`
_______________________________________________________
`E=(2x_1+x_2)(2x_2+x_1)`
`E=4x_1 .x_2+2x_1 ^2+2x_2 ^2+x_1 .x_2`
`E=5x_1 . x_2+2(x_1+x_2)^2-4x_1 .x_2`
`E=x_1 .x_2+2(x_1+x_2)^2`
`E=1+2(-10/3)^2=209/9`

\(A=\dfrac{\sqrt{x}+1+1}{\sqrt{x}+1}=1+\dfrac{1}{\sqrt{x}+1}>=1>0\)
=>A>|A|
Ta có: A= \(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)= \(1+\dfrac{1}{\sqrt{x}+1}\)
Vì x ≥0⇒\(\sqrt{x}\) ≥0⇒\(\sqrt{x}+1 \)≥ 1 ⇒ \(1+\dfrac{1}{\sqrt{x}+1}\)≥ 2
hay A≥ 2>0
Khi đó ta có: A=|A|
Vậy A=|A|

a. Em tự giải
b.
Phương trình hoành độ giao điểm (P) và (d):
\(-x^2=x+m-1\Leftrightarrow x^2+x+m-1=0\) (1)
(d) cắt (P) tại 2 điểm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=1-4\left(m-1\right)>0\Rightarrow m< \dfrac{5}{4}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=m-1\end{matrix}\right.\)
\(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{4\left(x_1+x_2\right)}{x_1x_2}+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{-4}{m-1}+m-1+3=0\)
\(\Rightarrow-4+\left(m-1\right)\left(m+2\right)=0\) (\(m\ne1\))
\(\Leftrightarrow m^2+m-6=0\Rightarrow\left[{}\begin{matrix}m=2>\dfrac{5}{4}\left(loại\right)\\m=-3\end{matrix}\right.\)
Vậy \(m=-3\)
a:
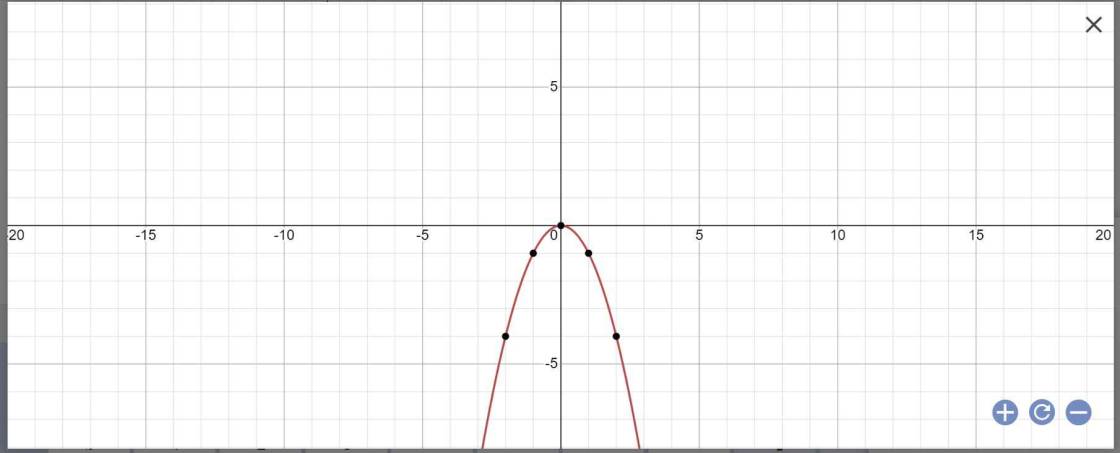
b: PTHĐGĐ là:
-x^2=x+m-1
=>-x^2-x-m+1=0
=>x^2+x+m-1=0
\(\Delta=1^2-4\left(m-1\right)=1-4m+4=5-4m\)
Để (P) cắt (d) tại hai điểm phân biệt thì 5-4m>0
=>4m<5
=>m<5/4
\(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+x_1x_2+3=0\)
=>\(4\cdot\dfrac{x_1+x_2}{x_1x_2}+x_1x_2+3=0\)
=>\(4\cdot\dfrac{-1}{m-1}+m-1+3=0\)
=>-4+(m-1)^2+3(m-1)=0
=>(m-1+4)(m-1-1)=0
=>(m+3)(m-2)=0
=>m=2(loại) hoặc m=-3

Câu 11:
PTHĐGĐ là:
x^2-x-m+1=0
\(\Delta=\left(-1\right)^2-4\left(-m+1\right)=1+4m-4=4m-3\)
Để (P) cắt (d) tại hai điểm phân biệt thì 4m-3>0
=>m>3/4
|x1-x2|=2
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2\)
=>\(\sqrt{1^2-4\left(-m+1\right)}=2\)
=>1+4m-4=4
=>4m-3=4
=>m=7/4

Đặt \(\left\{{}\begin{matrix}a=\left|x-1\right|\\b=\sqrt{y+2}\left(b>0\right)\end{matrix}\right.\)
Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}2a-b=4\\a+3b=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=2a-4\\a+3.\left(2a-4\right)=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=2a-4\\7a-12=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=2a-4\\a=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x-1\right|=3\\\sqrt{y+2}=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\\y=2\end{matrix}\right.\)
Vây...


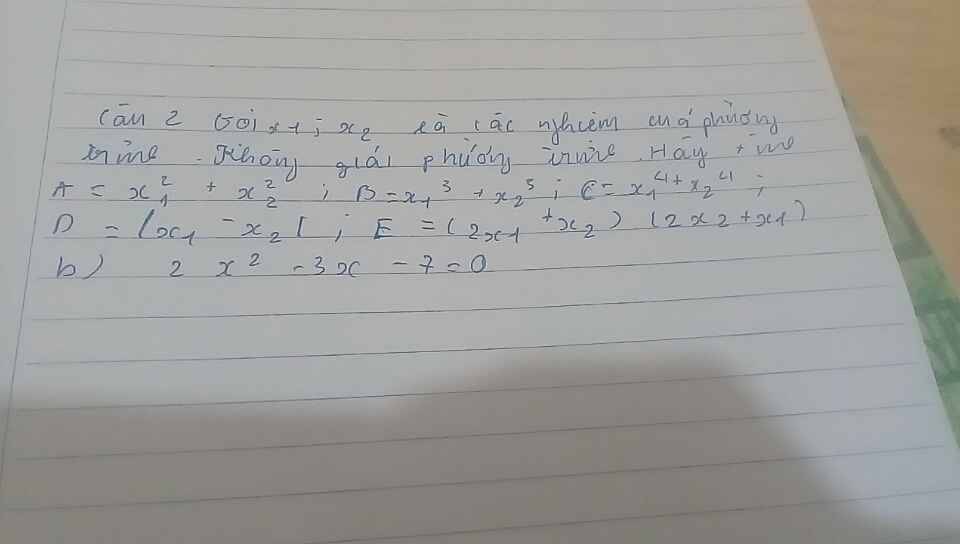
 giup minh cau nay voi
giup minh cau nay voi

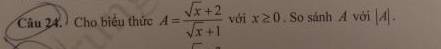
 giup minh cau nay voi
giup minh cau nay voi giup minh cau nay voi
giup minh cau nay voi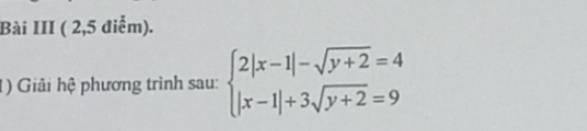
a.
Phương trình hoành độ giao điểm (P) và (d):
\(\dfrac{1}{2}x^2=-\dfrac{3}{2}x+2\Leftrightarrow x^2+3x-4=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=\dfrac{1}{2}\\x=-4\Rightarrow y=8\end{matrix}\right.\)
Vậy (P) và (d) cắt nhau tại 2 điểm có tọa độ là \(\left(1;\dfrac{1}{2}\right)\) và \(\left(-4;8\right)\)
b.
Phương trình hoành độ giao điểm:
\(\dfrac{1}{2}x^2=mx+2\Leftrightarrow x^2-2mx-4=0\) (1)
\(ac=-4< 0\) nên (1) luôn có 2 nghiệm trái dấu
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-4\end{matrix}\right.\)
Đặt \(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4m^2+8\)
Do \(m^2\ge0;\forall m\Rightarrow2m^2+8\ge8;\forall m\)
\(\Rightarrow P_{min}=8\)
Dấu "=" xảy ra khi \(m^2=0\Rightarrow m=0\)
a: Khi m=-3/2 thì y=-3/2x+2
PTHĐGĐ là:
1/2x^2+3/2x-2=0
=>x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=-4 hoặc x=1
=>y=1/2*(-4)^2=8 hoặc y=1/2
b: PTHĐGĐ là:
1/2x^2-mx-2=0
=>x^2-2mx-4=0
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(-4\right)=4m^2+16>0\)
=>PT luôn có hai nghiệm phân biệt
x1^2+x2^2
=(x1+x2)^2-2x1x2
=(2m)^2-2*(-4)=4m^2+8>=8
Dấu = xảy ra khi m=0