K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2021
Đặt \(f\left(x\right)=\dfrac{1}{3}x^3-x^2+mx+1\Rightarrow f'\left(x\right)=x^2-2x+m\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}x^2-2x+m\ge0;\forall x\ge1\\f\left(1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m+\dfrac{1}{3}\ge0\end{matrix}\right.\) \(\Rightarrow m\ge1\)
\(\Rightarrow m=\left\{1;2;3\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 6 2021
Không ai vẽ hình khi làm bài mặt cầu Oxyz đâu bạn, chỉ cần đại số hóa nó là được.
Gọi I là tâm mặt cầu, do mặt cầu tiếp xúc (Q) tại H nên \(IH\perp\left(Q\right)\)
\(\Rightarrow\) Đường thẳng IH nhận vtpt của (Q) là 1 vtcp
\(\Rightarrow\) IH nhận (1;1;-1) là 1 vtcp
Phương trình IH: \(\left\{{}\begin{matrix}x=1+t\\y=-1+t\\z=-t\end{matrix}\right.\)
I vừa thuộc IH vừa thuộc (P) nên là giao điểm của IH và (P)
\(\Rightarrow\) Tọa độ I thỏa mãn:
\(2\left(1+t\right)+\left(-1+t\right)+\left(-t\right)-3=0\)
\(\Rightarrow t=1\Rightarrow I\left(2;0;-1\right)\)
\(\Rightarrow\overrightarrow{IH}=\left(-1;-1;1\right)\Rightarrow R=IH=\sqrt{3}\)
Phương trình (S):
\(\left(x-2\right)^2+y^2+\left(z+1\right)^2=3\)
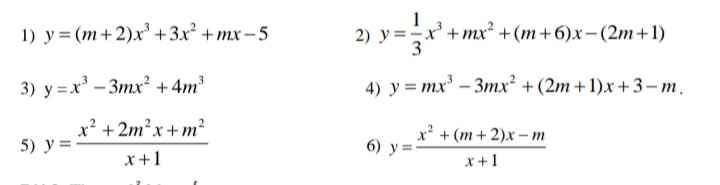
\(AB=\sqrt{SA^2+SB^2}=2a\)
Hệ thức lượng: \(SH.AB=SA.SB\Rightarrow SH=\dfrac{SA.SB}{AB}=\dfrac{a\sqrt{3}}{2}\)
Hệ thức lượng lần 2: \(SA^2=AH.AB\Rightarrow AH=\dfrac{SA^2}{AB}=\dfrac{a}{2}\)
\(\Rightarrow\dfrac{BA}{HA}=4\)
Mà đường thẳng BH cắt (SAD) tại A \(\Rightarrow d\left(B;\left(SAD\right)\right)=4.\left(H;\left(SAD\right)\right)\)
Kẻ \(HK\perp SA\Rightarrow HK\perp\left(SAD\right)\) (khá dễ chứng minh điều này, hiển nhiên \(AD\perp\left(SAB\right)\Rightarrow\left(SAD\right)\perp\left(SAB\right)\) \(\Rightarrow SA\) là giao tuyến của 2 mp vuông góc (SAD) và (SAB). HK vuông góc với giao tuyến nên vuông góc (SAD))
\(\Rightarrow HK=d\left(H;\left(SAD\right)\right)\)
Hệ thức lượng: \(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{AH^2}=\dfrac{16}{3a^2}\Rightarrow HK=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow d\left(B;\left(SAD\right)\right)=4HK=a\sqrt{3}\)