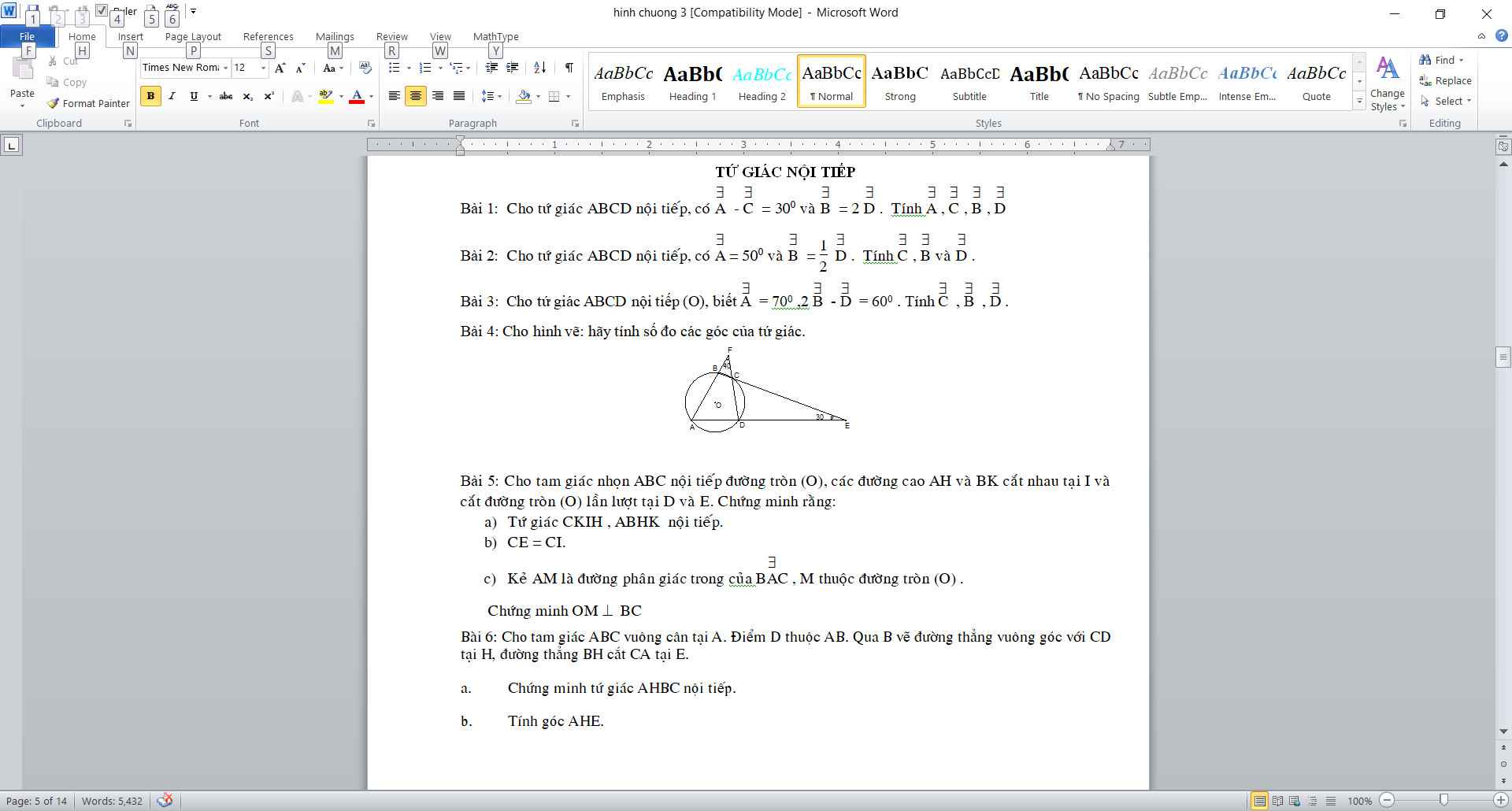
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 5:
a: Xét tứ giác CKIH có
\(\widehat{CKI}+\widehat{CHI}=180^0\)
Do đó: CKIH là tứ giác nội tiếp


\(a,\Rightarrow A=\dfrac{\sqrt{x}+1+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{2}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}\)
\(\Rightarrow A=\sqrt{x}\)
b, \(A=3\Rightarrow\sqrt{x}=3\Rightarrow x=9\)

b: Xét ΔAHC vuông tại H có HM là đường cao
nên \(AM\cdot AC=AH^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(HB\cdot HC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AC=HB\cdot HC\)


 giúp mk câu c
giúp mk câu c bài 2 tự luận câu c bài hình vs 2 bài cuối với ạ
bài 2 tự luận câu c bài hình vs 2 bài cuối với ạ giúp mình câu cuối với
giúp mình câu cuối với