K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
28 tháng 8 2021
\(x=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
\(y=\sqrt{3+2\sqrt{5}}-\sqrt{3-2\sqrt{5}}\)
Xem lại đề, \(\sqrt{3-2\sqrt{5}}\) không xác định.
2 tháng 7 2023
a: ĐKXĐ: x>0; x<>1
\(P=\dfrac{\sqrt{x}-1+1}{\sqrt{x}-1}\cdot\dfrac{1}{x-\sqrt{x}}=\dfrac{1}{\left(\sqrt{x}-1\right)^2}\)
b: Khi x=25 thì A=1/(5-1)^2=1/16
c: \(P\cdot\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{x}-1\right)^2=x-2005+\sqrt{2}+\sqrt{3}\)
=>\(\sqrt{3}+\sqrt{2}=x-2005+\sqrt{2}+\sqrt{3}\)
=>x=2005
1
0
9 tháng 10 2021
=\(\sqrt{2\left(12-6\sqrt{3}\right)}-\sqrt{2\left(28+10\sqrt{3}\right)}\)
=\(\sqrt{2\left(3-\sqrt{3}\right)2}-\sqrt{2\left(5+\sqrt{3}\right)^2}\)
=\(\sqrt{2}\left(3-\sqrt{3}\right)-\sqrt{2}\left(5+\sqrt{3}\right)=\sqrt{2}\left(3-\sqrt{3}-5-\sqrt{3}\right)\)
=\(\sqrt{2}\left(-2-2\sqrt{3}\right)\)=\(-2\sqrt{2}-2\sqrt{6}\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 3 2022
Nửa chu vi hình chữ nhật:14 cm
Gọi chiều dài hình chữ nhật là x (cm) với \(7< x< 14\)
Chiều rộng hình chữ nhật là: \(14-x\) (cm)
Diện tích ban đầu của hình chữ nhật: \(x\left(14-x\right)\)
Chiều dài hình chữ nhật sau khi tăng 1cm: \(x+1\)
Chiều rộng sau khi tăng 2cm: \(14-x+2=16-x\)
Diện tích lúc sau: \(\left(x+1\right)\left(16-x\right)\)
Do diện tích tăng lên 25 \(cm^2\) nên ta có pt:
\(\left(x+1\right)\left(16-x\right)-x\left(14-x\right)=25\)
\(\Leftrightarrow x+16=25\)
\(\Leftrightarrow x=9\left(cm\right)\)
Vậy hình chữ nhật ban đầu dài 9cm và rộng 5cm
TH
0
3 tháng 10 2021
\(A=\left(4x^2+2\cdot2\cdot\dfrac{1}{4}x+\dfrac{1}{16}\right)-\dfrac{1}{16}=\left(2x+\dfrac{1}{4}\right)^2-\dfrac{1}{16}\ge-\dfrac{1}{16}\\ A_{min}=-\dfrac{1}{16}\Leftrightarrow2x+\dfrac{1}{4}=0\Leftrightarrow x=-\dfrac{1}{8}\)
22 tháng 9 2021
Đề ko rõ ràng \(\sqrt{x^2}+x+\dfrac{1}{4}\) hay \(\sqrt{x^2+x+\dfrac{1}{4}}\)??
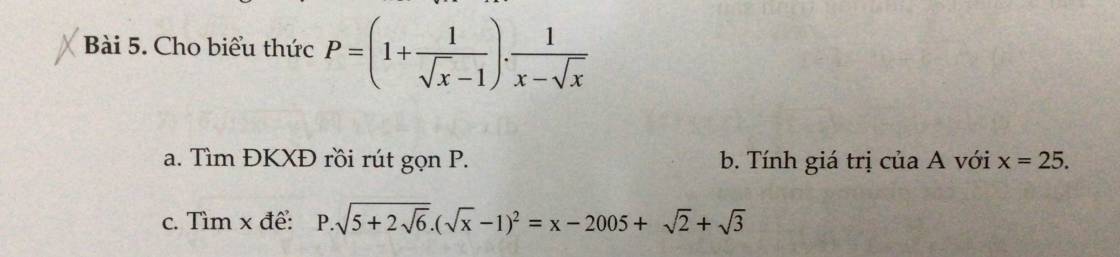
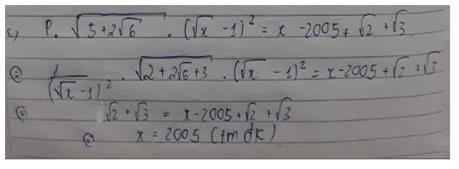
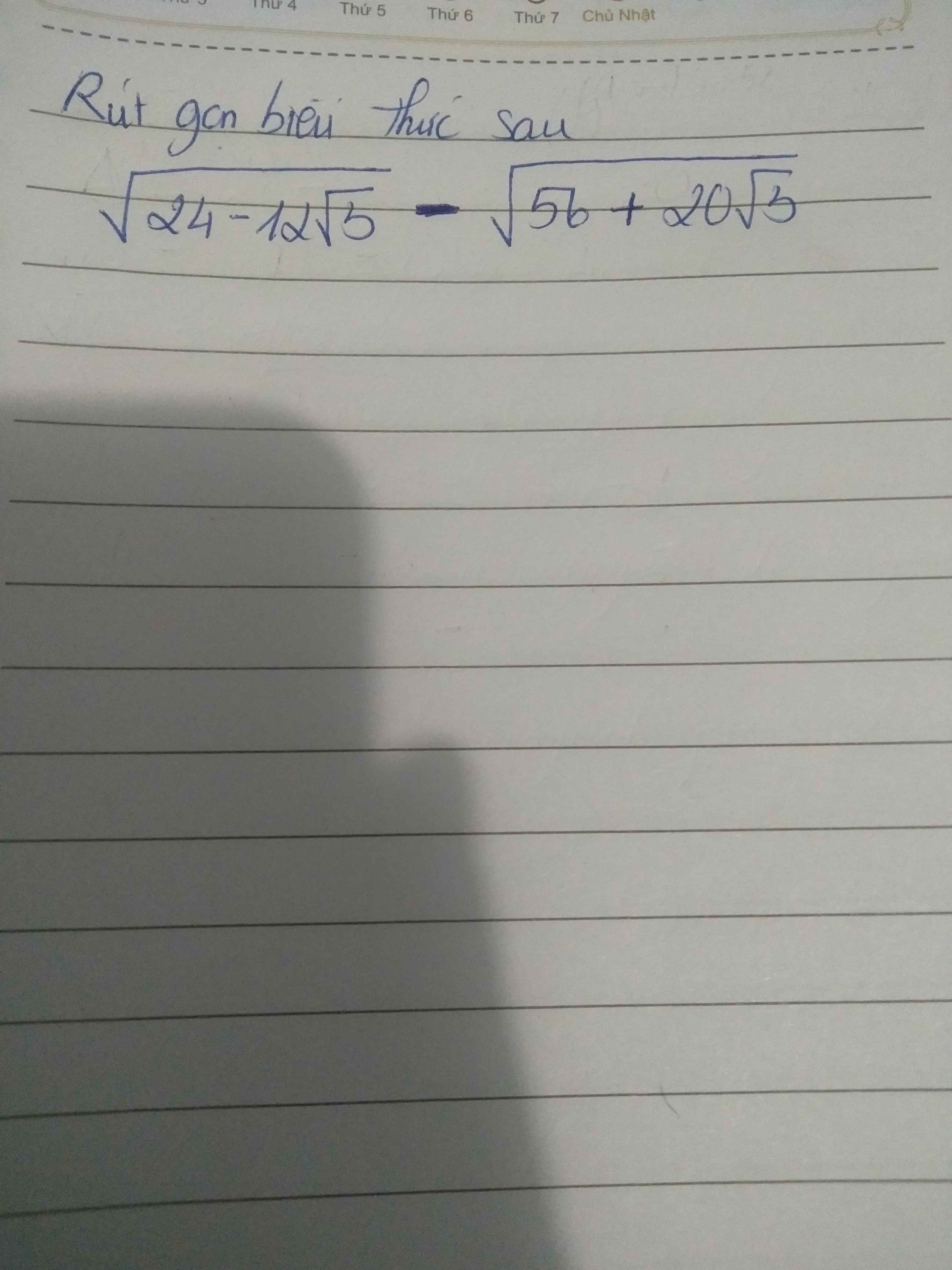
a: ĐKXĐ x>0; x<>1
\(A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{1}=\dfrac{x-1}{\sqrt{x}}\)
b: A<0
=>x-1<0
=>0<x<1