
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
b: \(MA=\sqrt{OM^2-OA^2}=R\sqrt{3}\)
=>\(AH=\dfrac{R\cdot R\sqrt{3}}{2R}=\dfrac{R\sqrt{3}}{2}\)
=>\(AB=R\sqrt{3}\)

b: Ta có: \(a=\sqrt{\dfrac{5}{2}-\sqrt{6}}\)
\(=\dfrac{\sqrt{5-2\sqrt{6}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{2}}\)
Ta có: \(P=1+\sqrt{a}\)
\(=1+\sqrt{\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{2}}}\)
\(=1+\sqrt{\dfrac{2\sqrt{6}-4}{4}}\)
\(=1+\dfrac{\sqrt{2\sqrt{6}-4}}{2}\)
\(=\dfrac{2+\sqrt{2\sqrt{6}-4}}{2}\)


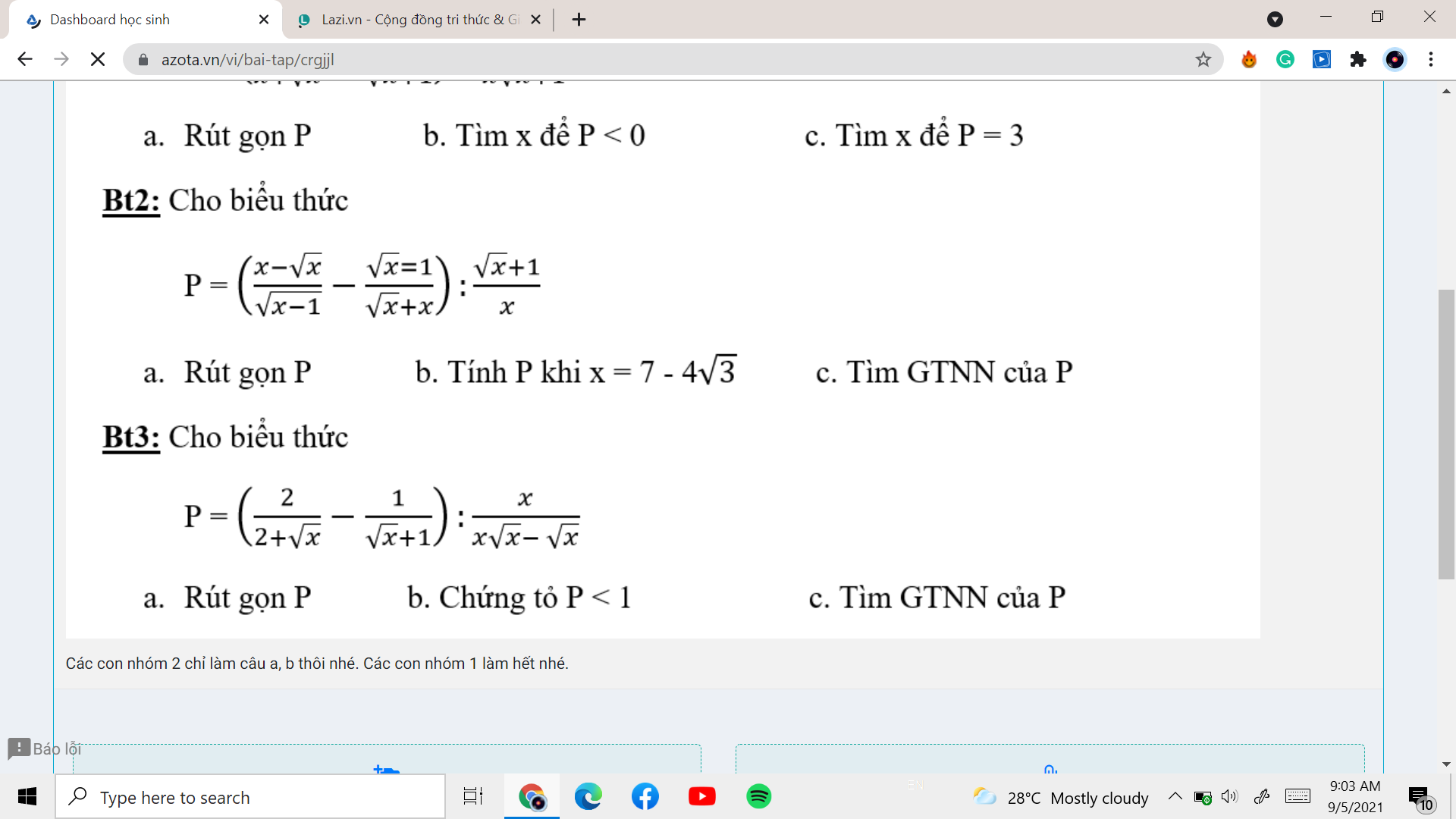
Bài 3:
a: Ta có: \(P=\left(\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{x}{x\sqrt{x}-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+2-\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{x}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)

a, Ta có BD , CE là các đường cao nên \(\widehat{ADH}=\widehat{AEH}=90^0\)
Tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=180^o\)
Suy ra ADHE nội tiếp đường tròn ( tổng 2 góc đối bằng 180 )
Ta có BD , CE là các đường cao nên \(\widehat{ADC}=\widehat{AEC}=90^0\)
Tứ giác BEDC có \(\widehat{ADC}=\widehat{AEC}=90^0\)
Suy ra BEDC nội tiếp đường tròn ( quỹ tích cung chứa góc )
b, Xét \(\Delta AEC\) và \(\Delta ADB\) có :
\(\widehat{ADB}=\widehat{AEC}\)
\(\widehat{A}\) chung
suy ra \(\Delta AEC\) \(\sim\) \(\Delta ADB\) ( g - g )
\(\dfrac{AE}{AD}=\dfrac{AC}{AB}\) \(\Leftrightarrow AE.AB=AD.AC\left(đpcm\right)\)
c, Bạn chụp cả đề được không, mình không đọc được đề


 giúp mình câu b bài 5 vs câu b bài 6 đi
giúp mình câu b bài 5 vs câu b bài 6 đi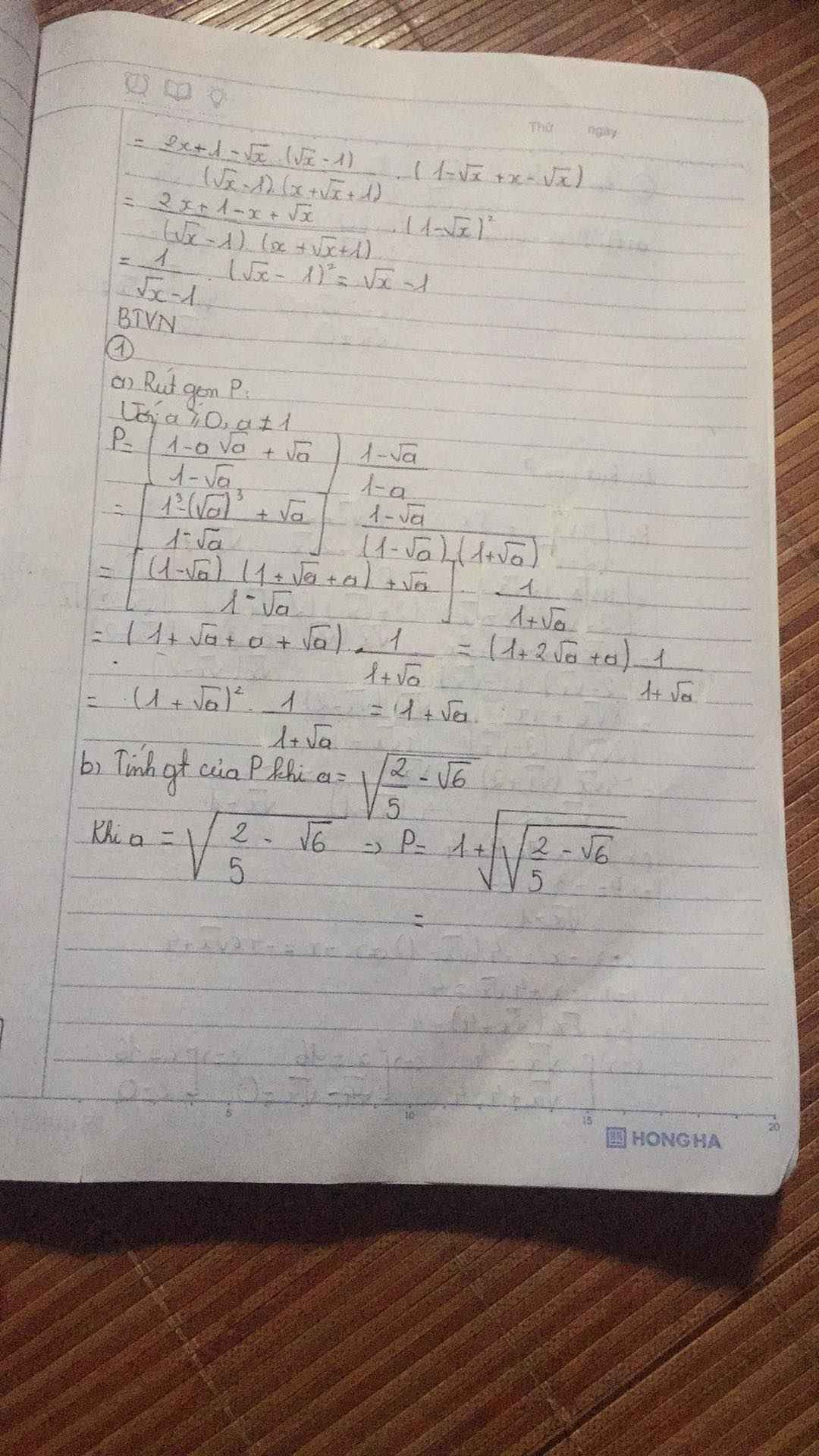

 Giúp mình bài 5 c nha
Giúp mình bài 5 c nha